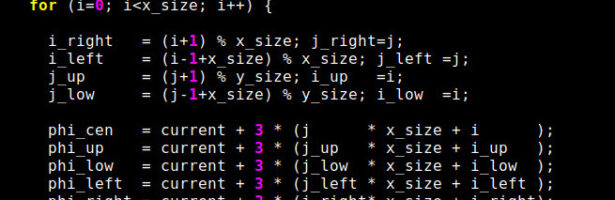
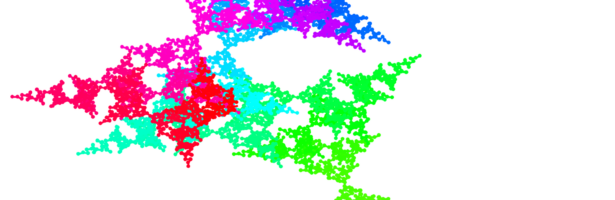
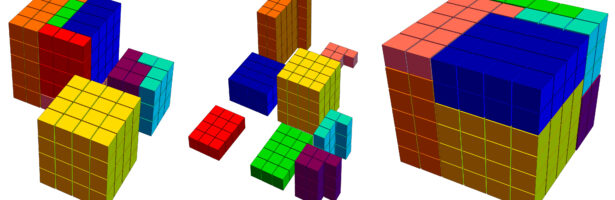
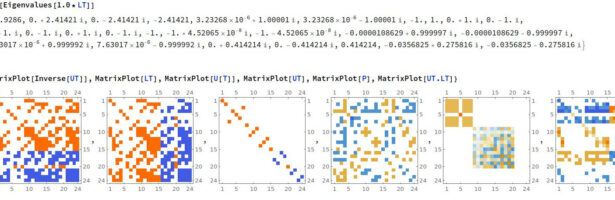
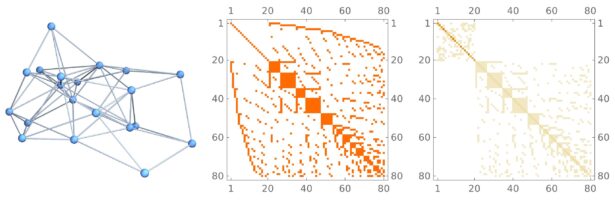
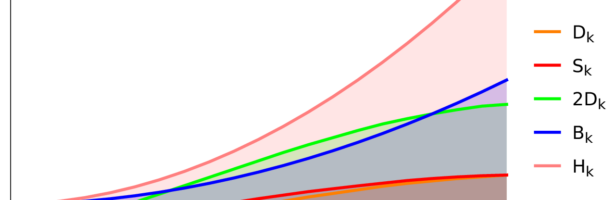
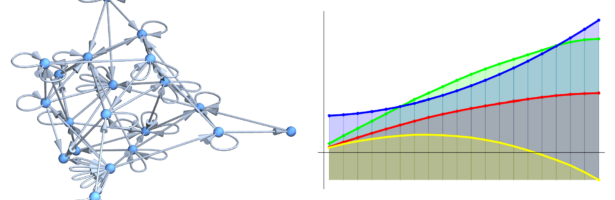
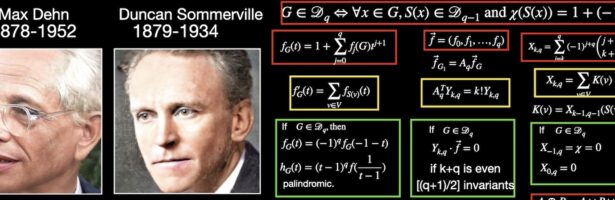
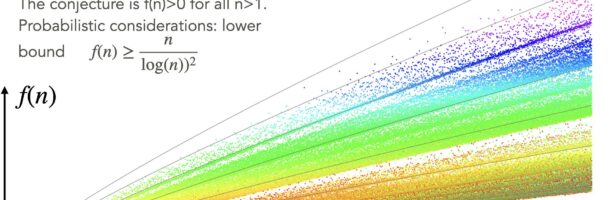
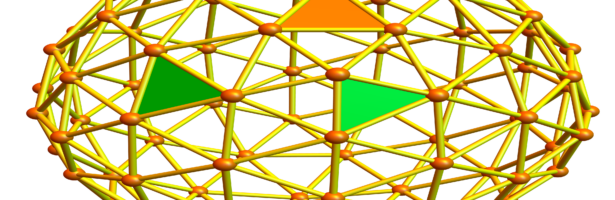
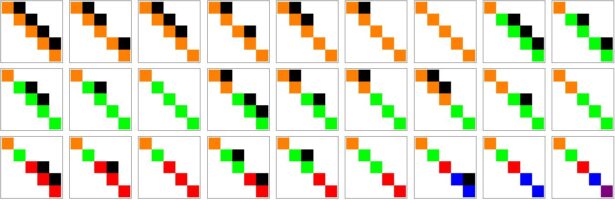
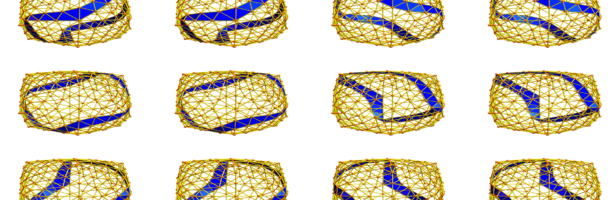
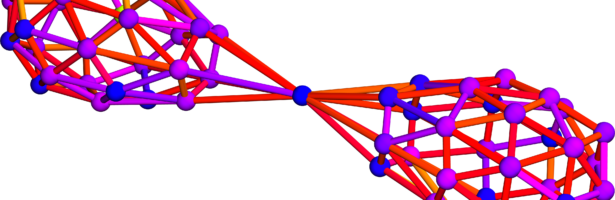
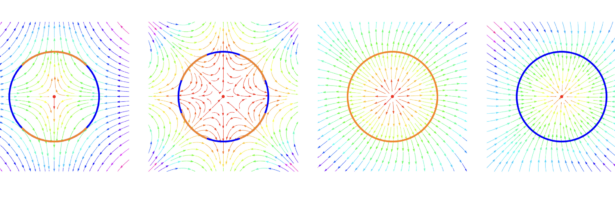
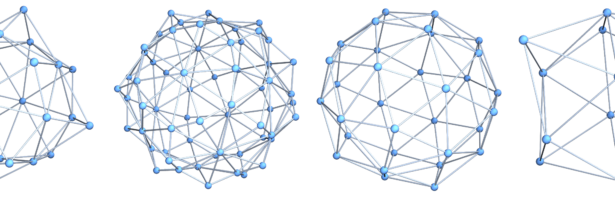
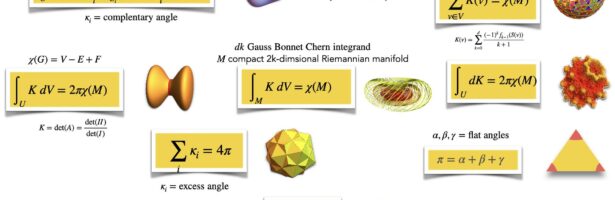
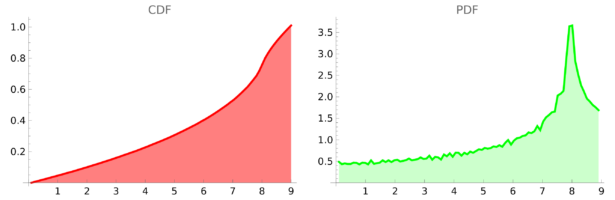
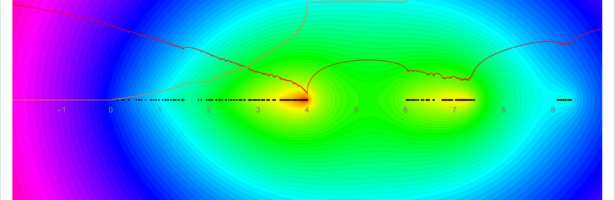
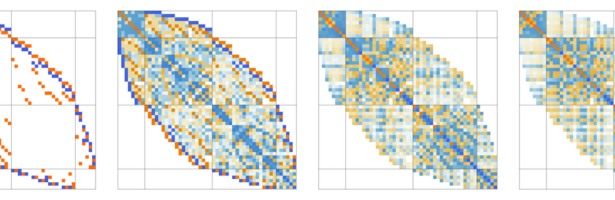
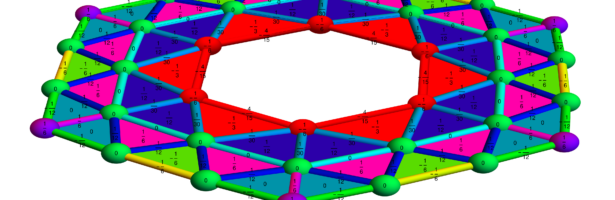
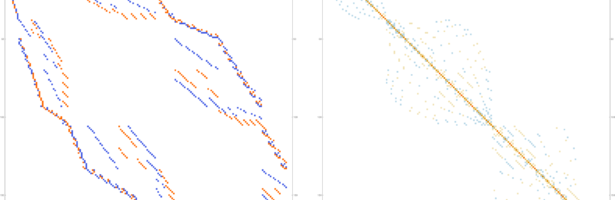
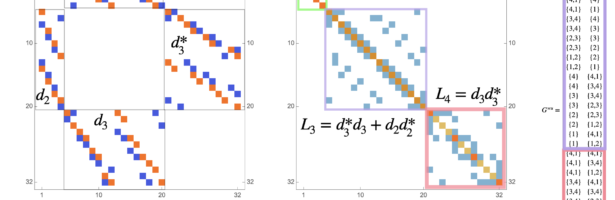
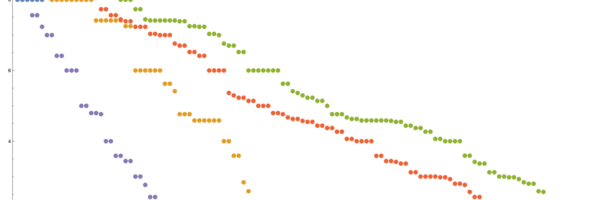
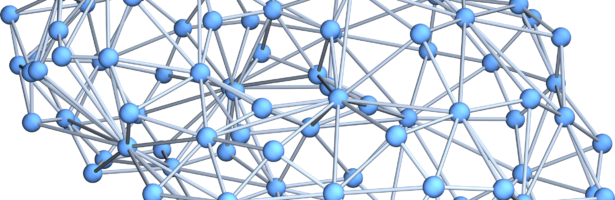
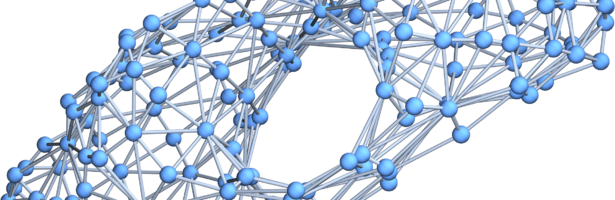
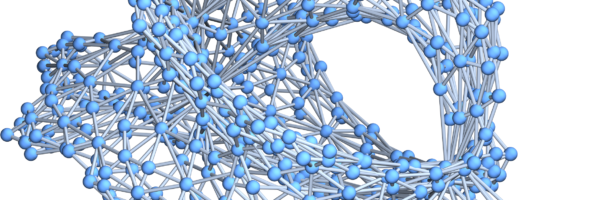
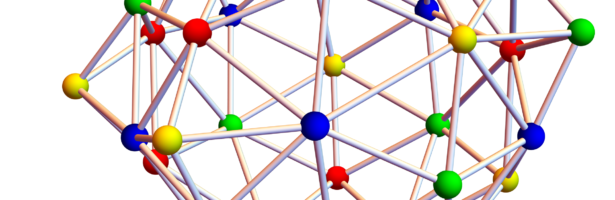
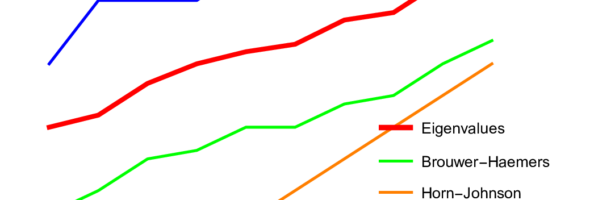
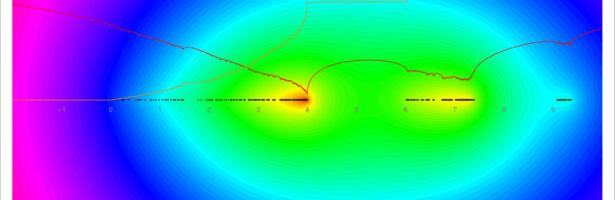
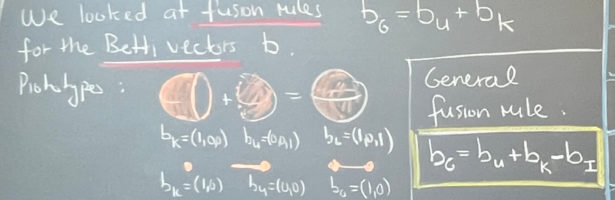Density of Wave Front on the Cube
If P is a light source on a cube we can look at , the wave front. Every point of this wave front can be assigned a group element, the rotation which is needed to rotate the initial Frenet frame at the start to the frame at time t. Whenever …