Quivers allow to model Schroedinger operators on graphs. With loops we can modify scalar values on vertices, with multiple connections, we can modify the magnetic part. This makes quivers attractive as well as theorems about quivers more interesting. An example was . In the talk last Saturday, I also mentioned the lower bound
. However, the lower bound works only for quivers without magnetic part. This means we attach just loops at a finite simple graph. Note that this class of non-magnetic quivers also has the property that a principal submatrix of its Kirchhoff matrix is again the Kirchhoff matrix of a non-magnetic quiver. In the talk, I gave the proof in the non-magnetic case but thought that the magnetic case follows. This is not the case. Take the graph with
for example which has eigenvalues
(as for all quivers without loops),\lambda_2=4$and
and
. The estimate $\lambda_1 \geq d_1-(n-1)$ does not work here.
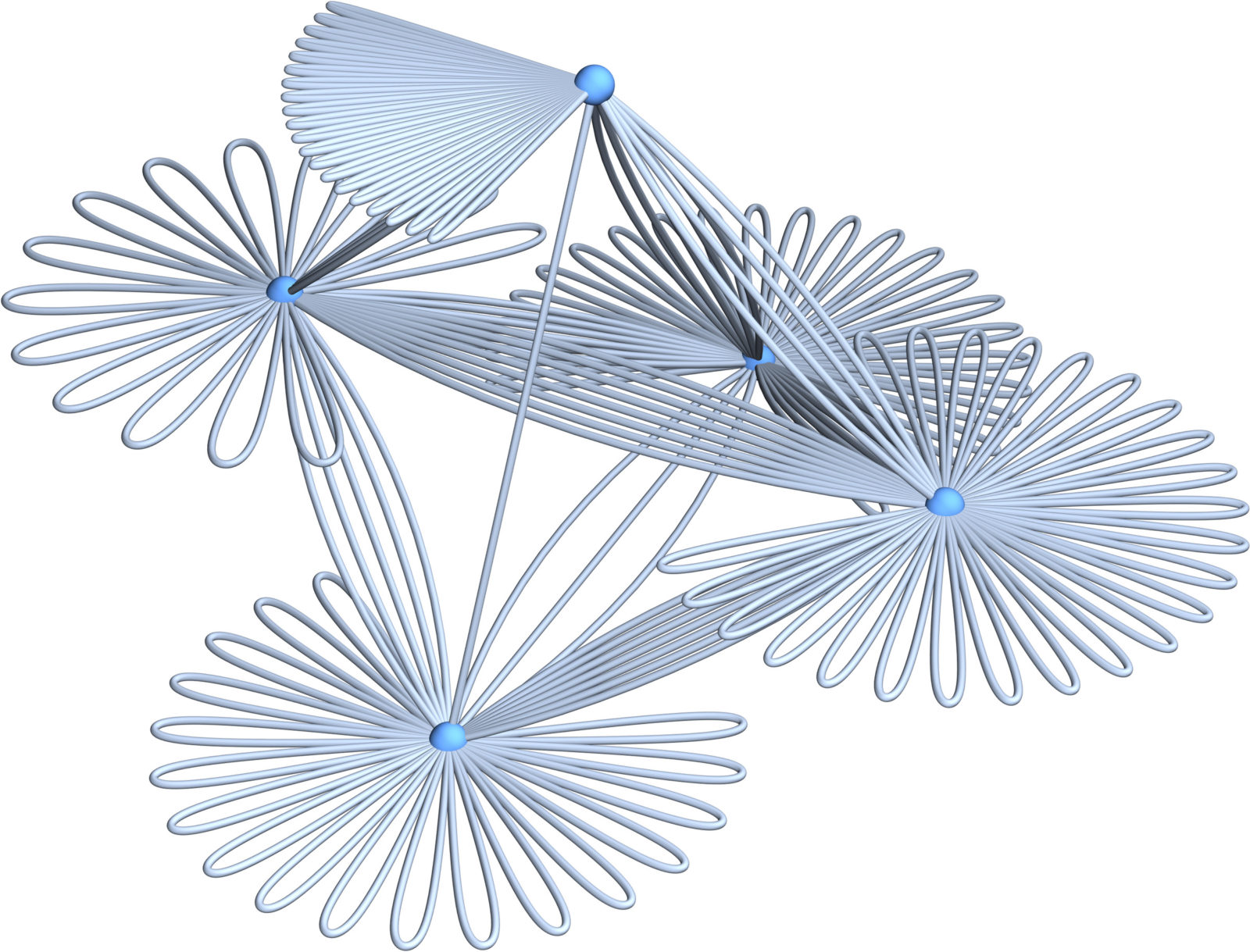
Update July 26. for the proof of the upper bound result quivers were the right structure. As just mentioned, it also gives a bit more general frame work allowing to put weights on edges or vertices and still get the same spectral estimates. As also mentioned in the talk, the upper bound for the eigenvalues allows to estimate determinants from above, unfortunately, one can not estimate with such estimates determinants from below. We would need to be able to estimate
from below but these are small divisor problems already in the simplest possible cases like almost periodic Jacobi matrices. The determinants depend in a subtle way on the rule generating the potential. The Jacobi case is the situation where the underlying graphs are cyclic graphs.
The first and last few seconds of the video show some experiments with a quite astounding photo camera. It follows me on my bike and while walking. On Monday, I recorded during a run.