A draft paper: https://people.math.harvard.edu/~knill/graphgeometry/papers/energyinequality.pdf. If we arrange the eigenvalues of the Hodge Laplacian of a sub-complex in a correct way, we get monotonicity of the eigenvalues. This is also very intuitive. More connectivity should produce more internal energy. Here is the code which is displayed in the paper (has already appeared in an earlier post)
[P.S. After writing the title and date April 1, I had spent a half an hour before the recording with searching for an April 1st statement and looked for approximations of the Feinstructure constant 1/0.0072973525628 in terms of the (in my judgement) four most popular Mathematical constants Pi,E,Phi,Sqrt[2] (one can certainly argue whether there are not more important ones but Pi,E, and the GoldenRatio phi are certainly on everybody’s list. As for Sqrt[2], it played an important role historically because of the first number which was established to be irrational). So, I wrote a little program which looked for the minimal distance of the grid Pi^a +E^b+Phi^c+Sqrt[2]^d and came up with E^2 + Pi^3 + GoldenRatio^9 + Sqrt[2]^9 It is not very good, the difference is -0.0000938111. The one line code which searched for it is at the end of this post (*). Why only 4 numbers? Because John von Neumann claimed once that he can fit with 4 parameters an elephant! ]
F[G_]:=Module[{l=Map[Length,G]},If[G=={},{},Table[Sum[If[l[[j]]==k,1,0],{j,Length[l]}],{k,Max[l]}]]];
s[x_]:=Signature[x];L=Length;s[x_,y_]:=If[SubsetQ[x,y]&&(L[x]==L[y]+1),s[Prepend[y,Complement[x,y][[1]]]]*s[x],0];
Dirac[G_]:=Module[{f=F[G],b,d,n=Length[G]},b=Prepend[Table[Sum[f[[l]],{l,k}],{k,Length[f]}],0];
d=Table[s[G[[i]],G[[j]]],{i,n},{j,n}]; {d+Transpose[d],b}];
Hodge[G_]:=Module[{Q,b,H},{Q,b}=Dirac[G];H=Q.Q;Table[Table[H[[b[[k]]+i,b[[k]]+j]],
{i,b[[k+1]]-b[[k]]},{j,b[[k+1]]-b[[k]]}],{k,Length[b]-1}]]; Betti[G_]:=Map[nu,Hodge[G]];
Beltrami[G_] := Module[{B=Dirac[G][[1]]},B.B]; nu[A_]:=If[A=={},0,Length[NullSpace[A]]];
Closure[A_]:=If[A=={},{},Delete[Union[Sort[Flatten[Map[Subsets,A],1]]],1]];Cl=Closure;
Whitney[s_]:=If[Length[EdgeList[s]]==0,Map[{#}&,VertexList[s]],Map[Sort,Sort[Cl[FindClique[s,Infinity,All]]]]];
OpenStar[G_,x_]:=Module[{U={}},Do[If[SubsetQ[G[[k]],x],U=Append[U,G[[k]]]],{k,Length[G]}];U];
Basis[G_]:=Table[OpenStar[G,G[[k]]],{k,Length[G]}];
RandomOpenSet[G_,k_]:=Module[{A=RandomChoice[Basis[G],k],U={}},Do[U=Union[U,A[[j]]],{j,k}];U];
G=Whitney[RandomGraph[{20,50}]]; U=RandomOpenSet[G,10];K=Complement[G,U];
KK=Beltrami[K];GG=Beltrami[G]; UU=Beltrami[U]; ev[L_]:=Sort[Eigenvalues[1.0*L]];
{EG,EK,EU}=PadLeft[Map[ev,{GG,KK,UU}]]; ListPlot[{EG-EK,EG-EU},Joined->True]And here is the picture which is produced. We took a random complex, a random complementary pair K,U of closed and open subsets and then display the differences of the energies. We see that for small energies, the gain of energy in the open and closed sets are the same.
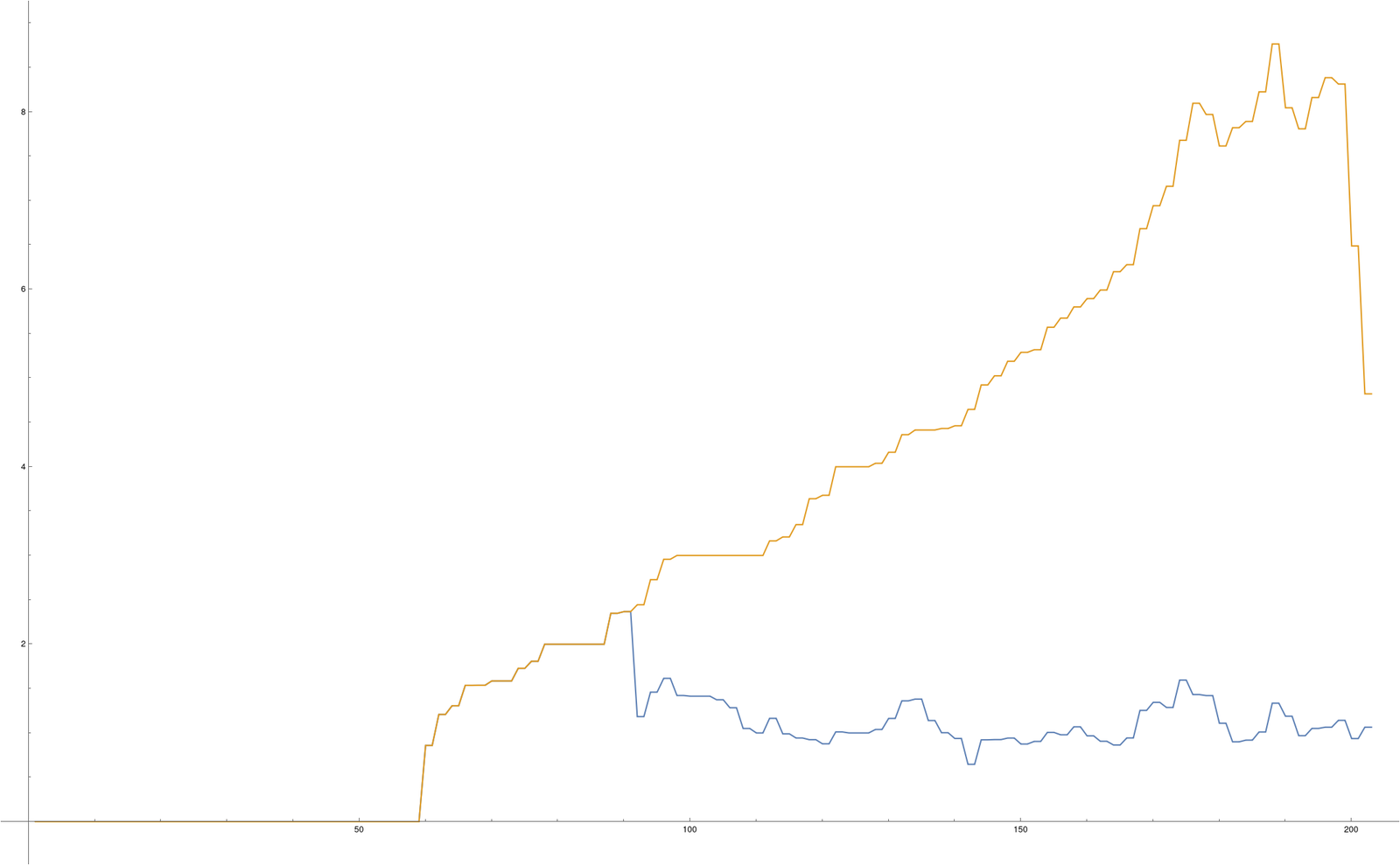
(*) As promised, here is the line which was used to find the April fools joke:
min=1000;feinstructure=0.0072973525628;n=10;Do[Do[Do[Do[min1=Abs[N[1/feinstructure-E^k-Pi^l-GoldenRatio^m-Sqrt[2]^h]];If[min1<min,min=min1;Print[{min1,k,l,m,h}];],{k,n}],{l,n}],{m,n}],{h,n}]
















