Brevity contributes both to clarity and simplicity. Surprisingly, it often contributes to generality. I myself am obsessed with brevity. I especially love short code. A short program is like a poem. If it is also effective, it can also be used as building blocks of larger programs. The Unix philosophy builds on this: produce small, effective programs like awk, grep, convert and use pipes as glue to combine them to larger programs. For me, the elegance of a language is measured on how short programs you can build and how readable they are. If a program is short and readable it is also easier to debug and verify. I started to code on small calculators (*) which is very inelegant: 129 lines of code were needed to program a simple mars landing game. The basic programming language on my first PC was a real relief. There one had to program in “spagetti Code” using GOTO loops. At college, I learned first PASCAL (**) of course as Niklaus Wirth (who died two weeks ago) hailed from ETHZ. (***) High level programming languages emerged in the context of computer algebra systems. Today’s CAS are much more than just algebra systems. Once you can effectively manipulate lists, you can handle anything. A movie for example is a pair {pictures,sound} where pictures is a list of pictures and sound is a pair of lists of amplitudes giving the left and right channel. A picture is a list of {red,green,blue} vectors with an indication how to partition the list to get a rectangle (****). To finish this introduction, let me mention that brevity and speed is not always the same. My obsession to brevity is partly also taught. See a story (*****).
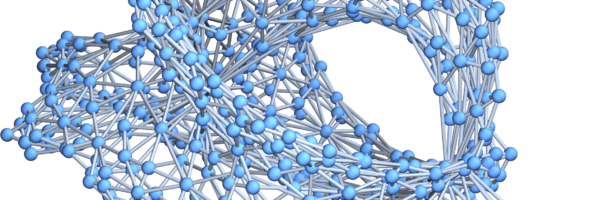
Let me give here the Mathematica code which illustrates my most recent theorem which was also the topic of this presentation posted on youtube. Here is the poem: (it can be copy-pasted also from the LaTeX Source, once the preprint appears on ArXiv). (Update: the arxiv version is now posted. Going to the LaTeX source there also shows the code. The ArXiv version can also serve as a reference).
Generate[A_]:=If[A=={},{},Sort[Delete[Union[Sort[Flatten[Map[Subsets,A],1]]],1]]];
Whitney[s_]:=Generate[FindClique[s,Infinity,All]];L=Length; Ver[X_]:=Union[Flatten[X]];
RFunction[G_,P_]:=Module[{},R[x_]:=x->RandomChoice[Range[L[Ver[P]]]];Map[R,Ver[G]]];
Facets[G_]:=Select[G,(L[#]==Max[Map[L,G]]) &]; Poly[X_]:=PolyhedronData[X,"Skeleton"];
AbstractSurface[G_,f_,A_]:=Select[G,(Sum[If[SubsetQ[#/.f,A[[l]]],1,0],{l,L[A]}]>0)&];
Z[n_]:=Partition[Range[n],1]; ZeroJoin[a_]:=If[L[a]==1,Z[a[[1]]],Whitney[CompleteGraph[a]]];
CJoin[G_,H_]:=Union[G,H+Max[G]+1,Map[Flatten,Map[Union,Flatten[Tuples[{G,H+Max[G]+1}],0]]]];
ToGraph[G_]:=UndirectedGraph[n=L[G];Graph[Range[n],
Select[Flatten[Table[k->l,{k,n},{l,k+1,n}],1],(SubsetQ[G[[#[[2]]]],G[[#[[1]]]]])&]]];
J=Whitney[Poly["Icosahedron"]]; G=CJoin[J,Whitney[CycleGraph[13]]]; p={2,2,3};P=ZeroJoin[p];
V=Ver[P]; F=Facets[P]; H=AbstractSurface[G,RFunction[G,V],F]; GraphPlot3D[ToGraph[H]]

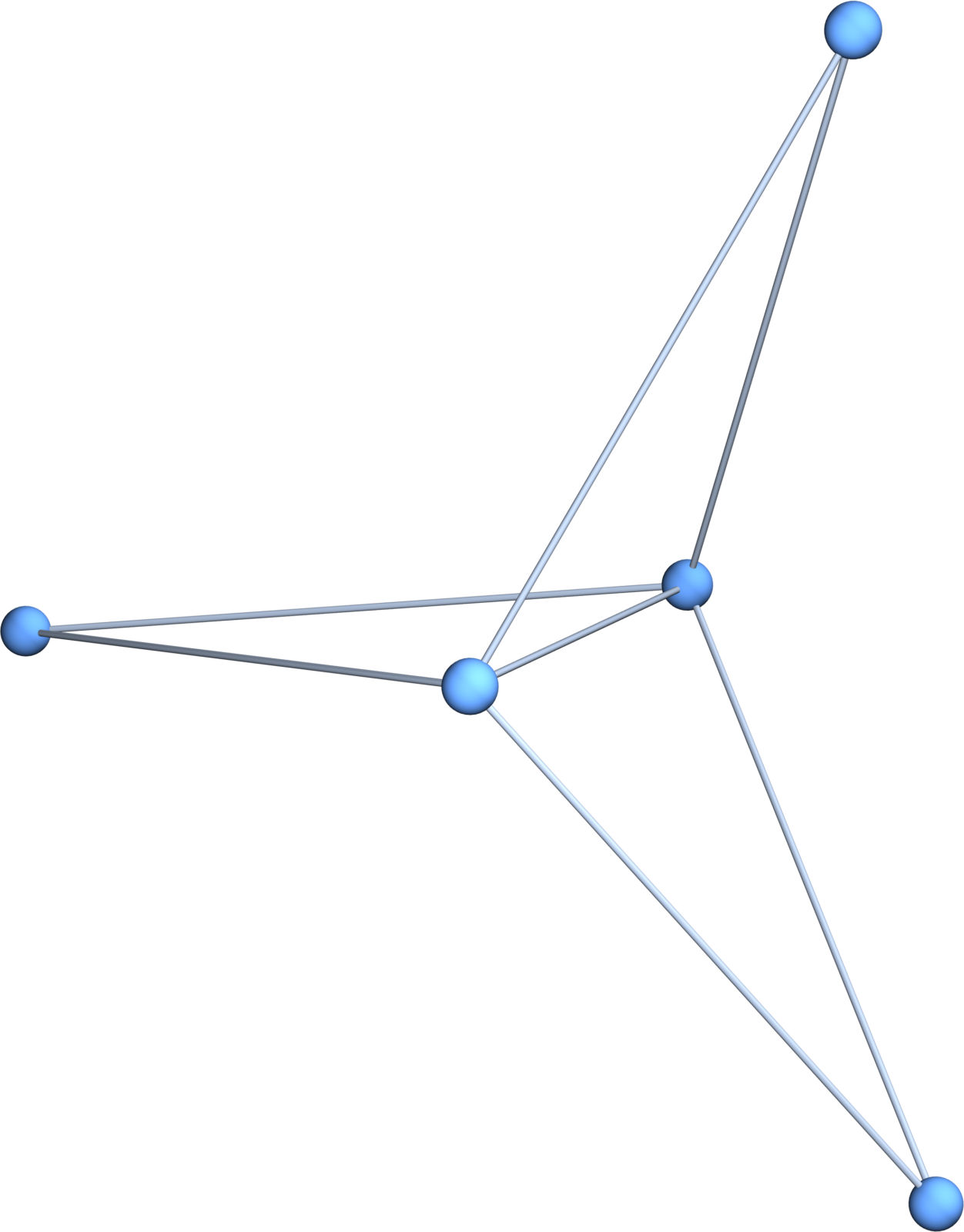
To the right of the program, you see its output. Of course, every time you run it it produces a new manifold as the function f is chosen randomly. In order to see what the poem does, one has to understand each individual line. The first line “Generate” generates from a set of sets a simplicial complex by closing it topologically (in the Alexandrov topology, a finite topology this is the closure). For example, Generate[{{1, 2, 3}}] produces a triangle, the simplicial complex {{1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}. If s is a graph, then Whitney[s] produces the simplicial complex of that graph. For example, let s=CompleteGraph[{1, 1, 3}] be the Windmill graph (seen to the right). Then, the Whitney functor produces the simplicial complex generated by {1,2,3},{1,2,4},{1,2,5}.. Indeed, Facets[Whitney[s]] would give a list of these three triangles. The procedure RFunction produces a random function from a simplicial complex G to a simplicial complex P. Such a function is always continuous in the Alexandrov topologies because the inverse of a closed set is closed so that the inverse of an open set is open. The core produced is AbstractSurface. I wrote it in such a way that it can be written in one line. Given the complex G (a manifold) and the function f and the facets, it takes all simplices in G which have as an image at least one of the facets F. The theorem tells that this is always a manifold, provided the complex P generated by the facets is a partition complex (coming from a multi-partite complete graph).
[(*) Footnote: When I started to program, first on TI 57 (and later on a TI 59, where small magnetic tapes allowed to permanently store programs) and wanted to play a mars landing game, I had to type in by hand dozen of assembler type code (you can see my own mars landing program here, for a TI59 hardware hacked so that the game could be played with a joy stick) . Programming in assembler instructions required to manipulate the individual memory parts of the computer. (By the way, I just remember, that Daniel Stieger , who was in a parallel class at the Schaffhausen Highschool (PDF) and who was certainly the best programmer among all the high school students during that time (at least among the students I knew), managed to hack into the machines to reprogram the EPROMS of these TI calculators. He showed us that after entering a secret backdoor key combination, one could reprogram the guts of the calculator, so that pushing a button like the square root button would do something else. I myself only hardware hacked these computers, soldering in an interface to be use an external joy stick for playing games. The screen of these calculators had 1 line, but on a TI 59 with a printer, you could print line after line and so play by seeing the output plotted.]
[(**) Footnote: During plenary lectures for the mandatory “Programming” courses, with hundreds of students, the specifications of the language would be written on the board during plenary lectures, with hundreds of students. The professor was Peter Laeuchli (1928-2021) a student of Eduard Stiefel who also was a student of Heinz Hopf. The lectures were actually quite entertaining. Lauechli would at the time be interested in programming music and showed off some of his programs. Many of my teachers (starting with my high school teacher Roland Staerk who was a student of Beno Eckmann, a student of Heinz Hopf) or Ernst Specker (my linear algebra and logic teacher), Urs Stammbach (my Algebra I,II teacher), Guido Mislin (my Lie groups teacher), Hans Laeuchli (my model theory and non-standard analysis teacher), Erwin Engeler (my topology and mathematical software teacher) or Max-Albert Knus (my commutative algebra teacher) are kids or grand-kids of Hopf. And countless many course assistants (more than a dozen) were graduate students from one of these Hopf descendants. From the computer science point of view, Eduard Stiefel (whom I never met, he had passed already when I enrolled to ETH) was the person at ETH branching into computer science, founding the applied math institute at ETHZ (still being a great topologist (Stiefel-Whitney class is named after him)). By the way, computer science only split during my student time from the math department. If I had graduated one year earlier, I could also have had a degree in computer science (there had been a transition period where mathematicians could also get the computer science degree). I got introduced to more modern programming languages in a course “mathematical software” taught by Erwin Engeler (who would teach us Lisp, a language which inspired Mathematica, where everything is based on lists too) and later course assisted in computer science under Roman Maeder (who is also a descendant of Hopf) and who was one of the early pioneers in Mathematica, which had prototype versions being tried out by computer science students. We used Magma (then still called Cayley), Macsyma and Reduce. I could see Mathematica work already before its first release as some of the graduate students in computer science had access. It was magic for me, especially because it allowed to write so short programs. Position[Map[IntegerQ,Sqrt[Map[Prime,Range[1000]]-1]],True] for example tells which of the prime numbers p(k) are of the form n^2+1. As 12 appears, p(12)-1=37-1 is a square.
[(***) Footnote: I only learned now while writing that Niklaus Wirth died on January 1st of this year 2024. Wirth would not only design the very beautiful Pascal language, but create other languages like Modula or the very impressive Oberon. During my graduate student time, I also had quite a bit of contact with computer science PhD students and professors, especially through military. I was lucky to get into the Swiss cryptology group, where in WK’s (repetition courses) we would be in a beautiful place in Switzerland and work on cryptology. There were three groups computer scientists, statisticians and mathematicians. I was in the mathematicians group. An other member wasRoman Maeder (who would bring his Next Workstation to these camps. That machine completely blew me away and prompted me to shell out 6000 dollars (I already got course assistant salary as an undergraduate and was well payed as a graduate student) (today that would be at least twice in comparison) to buy my own Next Workstation. Maeder also wrote eye-opening and beautiful books on Mathematica explaining the paradigms of this high level programming) or Ueli Maurer, who would de-facto lead the group, as he was already then a top cryptology expert in Switzerland. Or Marcel Griesemer, (I think it was him, who once showed us Oberon. The entire operating system would fit on a “floppy” including the compiler. The editor alone was impressive as the fonts could be little animated figures). While I am impressed with the creativity of Wirth to build new languages, it is also sad, that he abandoned PASCAL. Pascal was such a nice language. During our cryptology WK’s (WiederholungsKurs = repetition course) we would program in Turbo Pascal (we implemented for example all the integer factoring algorithms, I myself together with Beat Scherer (a graduate student of Specker) programmed the Pollard Rho and Morrison-Brillhard and quadratic sieve. If Pascal would have been developed further, like for example allowing directly working with the memory (as C does), it could have played the role of C today. Pascal was pretty fast. I once wrote a program for my Atari ST in Pascal which would interact directly with my E-piano using midi interface. The program was fast enough to analyze what I play and play back modified replies in real time allowing me to have an AI piano partner. Today, my workstations are thousand times faster and stronger but I often feel that the Atari ST was more responsive often than our modern bloated windows managers (I used Blackbox or fluxbox for almost 20 years) but it started having problems a few years ago, I currently use xfce4 which is still too bloated. I’m still not friends with monsters like Gnome or the rigid Ubuntu desktop. UI designers should realize that the most forbidding thing is latency. Even fractions of a second are annoying. Even the quite nice Apple OS, sometimes can lock out the user for fractions of a second. You never, ever should see a turning wheel. The Atari ST had no lag! And even my TI 57 was more responsive than a modern million times stronger machine today.

[(****) Footnote: Here is an example of a 2 x 2 pixel color picture: P3 2 2 255 200 0 0 0 200 0 0 200 0 0 0 200 . The P3 tells that it is a PPM format in color. The next two numbers tells that it is a 2-2 picture. Then comes the maximal amplitude 255. Then come 4*3 = 12 values. The first three numbers 200 0 0 give a red pixel, then comes a 0 200 0 green pixel (we finished the first row). Then comes a green pixel and finally again a red (200 0 0) pixel. I stored this as a file example.ppm. Now, I can write convert -thumbnail 1000 example.ppm example.jpg . And here to the right you see the picture: You see everything is just given by a list of numbers. So, you do not need any programming skills to write pictures. You just need to be able to write a text file or edit a text file and then you can convert it into any possible file format. The image magic program convert can essentially handle any format. Here is something you can do on the command line to get a 4K image example.jpg from these 4 pixels:
echo "P3 2 2 255 200 0 0 0 200 0 0 200 0 0 0 200">example.ppm;
convert -thumbnail 3840 example.ppm example.jpgAnd if you are really obsessed with brevity as I am you can even simplify this more and reduce the above 2 lines to 1 line. The amplitude 255 can be changed to 1. A 43 character expression now produces a 4K resolution picture.
echo "P3 2 2 1 1 0 0 0 1 0 0 1 0 0 0 1">s; convert -thumbnail 3840 s s.jpg[(*****) Footnote: Here is an episode about the balance between “brevity” and “speed”. In our programming courses in college (which every mathematician had to take and pass), we had also to write programs of course. We were mostly programming on the Apple II computers in Pascal and at one point had to submit also programs using punch cards (a numerical integration program for solving differential equations. This was painful because one had to wait for getting the result back from the main frame computer. A simple typo would cost you hours. The Apple programs were stored on large 5 + 1/4 inch floppies. We were also tested in programming. Some exam problems were to write on paper a Pascal program. I remember one of the problem session seminars (organized by graduate students), where the home works were discussed. I remember well, how one of the CAs once announced “And here is an example on how not to program. It is a program by Oliver Knill” and then he displayed my program and discussed why it was so bad. I don’ t remember the specifics but that my program was unnecessarily long and convoluted, checking various cases and depending on the case did things differently. The program was not elegant, but it was fast! This is rather typical in engineering: a general algorithm can be beautiful and simple but not effective. Lets look at the procedure “FactorInteger” or “PrimeQ” checking for primes. Mathematica does not give much details on what algorithms are used but it is definitely something complicated. If the number is small, one can do use the Baby algorithm. Here is my own example implementation, giving all the primes up to 1000.
MyPrimeQ[n_] := Union[Map[IntegerQ, n/(Range[n - 2] + 1)]] == {False};
Flatten[Position[Map[MyPrimeQ, Range[1000]], True]]Yes, it is elegant; but it is also terribly ineffective. It can be improved by replacing Range[1000] with 2Range[500]+1 giving only the odd primes and then add the only even prime before. It can also be improved by replacing Range[n-2] +1 with Range[Floor[Sqrt[n-1]]] because factors can not be larger than the square root of n. It can then further improved by taking only numbers of the form 6k+1 or 6k-1 and adding the primes 2,3 separately. Now, what Mathematica probably does is to use some sort of pre-sieving checking for small prime factors up to some range, then use the Baby test in a larger range, then use Pollard Rho up to some bound, then use other tools like Elliptic curve pollard, then use Morrison-Brillard, then use the quadratic sieve, then use the number field sieve. The entire code for “FactorInteger” is probably several thousand lines long. it is not short but it is fast. The above code for MyPrimeQ is poetry as it is elegant and everybody can see in a second, what the program does and that it is correct. Indeed, it just tests whether n is divisible by numbers 2,3,4,…,n-1 and if all answers are False , it knows that n is a prime. Note that the program does not need to loop. Niklaus Wirth had been fanatic to get rid of the “Goto philosophy” which was central in BASIC but led to Spagetti code. Everything could be done with While or For loops. Later, Wirth would even get more pure (fanatic) and get rid of For loops. Indeed, one can do everything with While. With the LISP paradigm one can get rid even of While. We just produce lists and work directly on lists. Range[100] for example produces the list of the first 100 integers. Sin[Range[100]]] produces directly the list of first 100 numbers sin(n) without having to loop. This works also in higher dimension But again, while this is elegant, one could not program something like FinalCutPro using this paradigm. Final Cut Pro projects are hundreds of gigabytes long (even small projects). For a one hour movie with various footage sources, one can easily get into the tera byte range. Now, it is completely impossible to get all these files into memory and work on those “lists”. What the programming language C allows to do is directly work with the memory. We need to loop over intervals of memory and this needs to be done carefully so that one does not get into Memory allocation problems.
One should add that the loop less approach is not always the best or most elegant. Lets look at the problem to write down the 10×10 multiplication table learned in 1st grade: Making a table is the fastest MatrixForm[Table[x*y,{x,10},{y,10}]] and most elegant. The loopless approaach is fist to generate a list of all pairs Tuples[Range[10],2]], then we define f[{x_,y_}]:=x*y; and apply this to the pairs, then partition and show the matrix MatrixForm[Partition[Map[f,Tuples[Range[10],2]],10]] . No loops were used but an iterated loop was definitely faster. By the way, when I program myself, then I often write the code in a first state using loops. This allows often to debug things better at first. Then, once it works, I try to make it shorter by getting rid of the loops. The example code above for the manifolds from partition paper was more elegant than the code produced for “Discrete algebraic sets in discrete manifolds” where I used some looping.