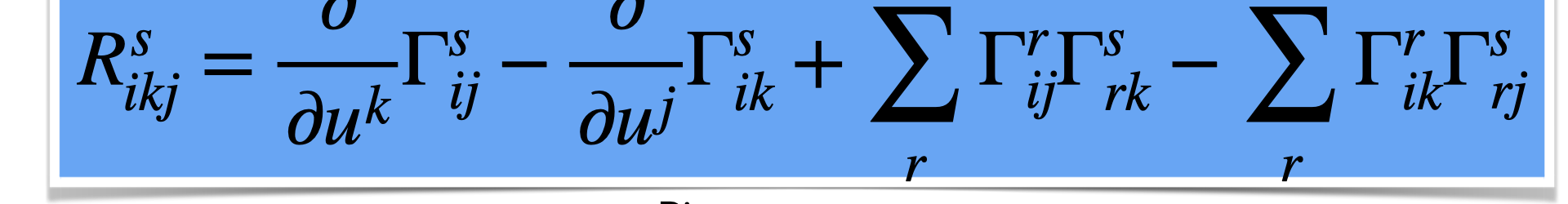
General relativity plays on a pseudo Riemannian manifold (M,g). The Einstein equations 
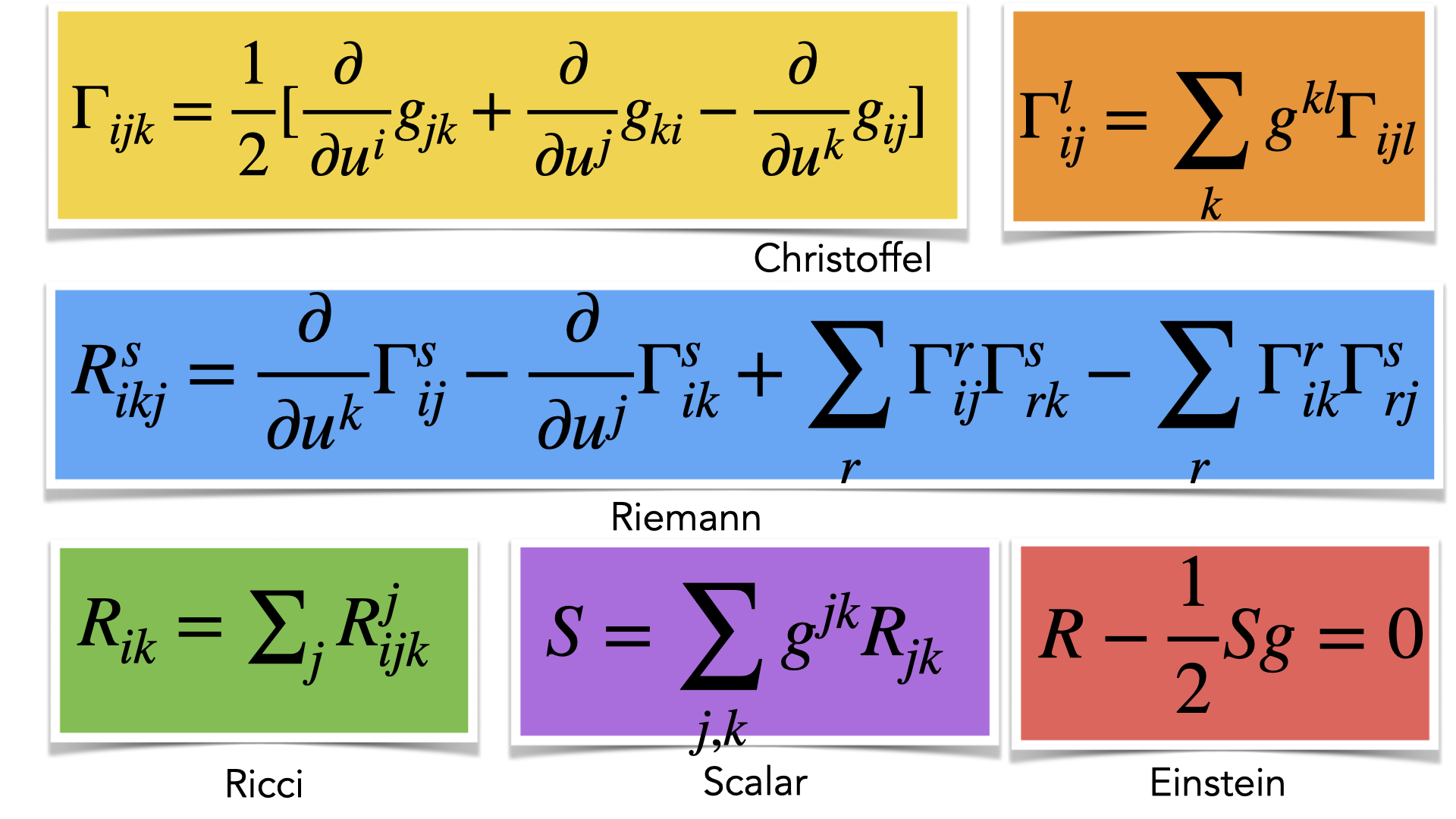
A popular textbook is “gravitation” by Misner-Thorne-Wheeler. (Misner and Thorne are academic kids of Wheeler). My favorite is still the GR book of Choquet-Bruhat as it gets faster to the point. (Wheeler by the way is my academic grand-grand father like for about 1700 other mathematicians)). The computations in differential geometry are usually quite heavy, even in simplest situations. More geometric, physical or numerical insight is needed to appreciate the theory. For two dimensional manifolds, the story is covered in “elementary differential geometry” as every two dimensional Riemannian manfold is an Einstein manifold, given that the Ricci tensor R is just K times the Riemann metric g, where K is the curvature. The arena of general relativity is a four dimensional Lorentzian manifold (M,g). In some sense GR in 2 dimensions is trivial as it forces the matter tensor to be zero.
First of all it is important to state that the theory presented in textbook is rather incomplete. When describing the motion of matter in (M,g), one neglects that the mass itself contributes to the tensor T. This usually does not come up. One just realizes how nasty the set-up is if one looks the motion of two bodies like two black holes spinning around each other. One can not just assume that each black hole moves as a geodesic in a fixed Riemannian manifold as the Riemannian manifold is determined by these two bodies. Mathematically if one takes two point masses (it does not have to be black holes), then one usually treats them as points so that in space time, one has mass concentrated on one dimensional curves (which are singular and not smooth). Assuming two bodies alone like the earth and the sun and just assuming the laws of general relativity without assumptions there is no law which describes the data (G,g,T) as T is entirely made up by the curves in space time traced by the particles and g is determined by that but that the geodesic paths assume a fixed metric g. The uglyness of this incomplete theory only comes up when trying to compute the motion of a 2 body problem, which boils down to a numerical scheme where one makes lots of assumptions, like even Newtonian approximations. One usually also neglects gravitational waves which complicate the theory even more as the gravitational waves should also be part of the overall metric g. Texbooks just linearlize and it seems to work well as LIGO data have shown. Still, what one would dream about as a mathematician is a variational principle which would give us a space time manifold (M,g) that describes the motion of two particles spinning around each other including all the gravitational waves and the motion of the two bodies. That this is not possible is a bad sign. Only the one body solution is known and this is the Schwartzschild metric which by the way explains all the experiments one has made to verify the theory. A non-perturbative frame work for a solution of the 2-body problem has not even emerged. So, one has tried other approaches, one of them is a discrete version.
A discrete theory of general relatiivty is Regge calulus. It comes from the 1960ies and is in Chapter 42 of “Gravitation”. It is very natural but old fashioned as it uses the underlying geometry and so angles and areas from the geometric realization of the discrete geometric structure. For me this is just unacceptable for various reasons and shows that the theory is essentially a numerical approach. Numerical schemes almost everywhere in mathematics are ugly. Look at integration schemes in integration or for differential equations, not to speak from numerical schemes in partial differential equations which is always a patchwork of “hacks” getting around the fact that naive and beautiful discretiszations are numerically unstable or even chaotic. One of the simplest examples is the discretization of the pendulum equation 
So, take a finite abstract simplicial complex (a discrete 4 manifold) and follow Regge: (0,2) tensors like the metric g or the Ricci tensor R or the matter tensor T are just functions on the set of triangles. The Ricci value B(x) for a triangle is in the simplest case just the length of the dual sphere of x which is the intersection of the three unit spheres S(a),S(b),S(c) of the triangle x=(a,b,c). The area of the triangle in the simplest case is just1. The Einstein equations in this case would state that the length of the dual sphere is constant. This is of course too rigid. We need flexibility to incorporate more general Riemannian metrics and so Ricci tensors. As I have advocated now for more than 10 years (following of course by existing similar frame works in classical mathematics) is to see curvature or length integral geometrically. It is nice that both pillars of relativity, the Einstein field equation part as well as the geodesic part both not only can be described by variational principles but also integral geometrically. Integral geometry cuts though terrible constraint considerations like (which angles are allowed in a geometric frame work, how to embed a network in space etc etc. Reading chapter 42 (this was before the Adams Hitchhikers guide to the galaxy!) in “Gravitation” shows how one has to fight in doing so. No wonder the theory never really took off. Nobody computes gravitational waves from Sag*A using Regge calculus despite the fact that the theory is 60 years old. In the talk last Saturday, I just tried a bit to outline what I think would be a good approach. And it looks quite elegant as the functional looks as something very natural as 
