If G is a q-manifold, we have defined a geodesic dynamics T on the frame bundle P, a principle fiber bundle with structure group . As we have seen last time, the geodesic update step
, where
is the dual sphere of the
-simplex
. Everything is finite. G is a finite set of non-empty sets closed under the operation of taking finite non-empty subsets. The manifold assumption assures that every unit sphere
is the join of the stable sphere
(the boundary sphere of the simplex x) and the unstable sphere
. The geodesic dynamics can easily be extended to manifolds with boundary. We just, when reaching the boundary use the dynamics on the boundary for one step. It is cool to see that the dynamics on a geodesics can be seen as a billiard within a tube. For a two dimensional tube we need two steps to advance one, in a three dimensional tube (the standard crane construct), we need three steps. By the way, every subset of the dual complex
defines a manifold with or without boundary.
Here are some examples of geodesic paths using the reflection law (billiard). It is interesting to get periodic orbits in the interior which are caught be a non-flat interior. In such relatively regular situations (I took also soft barycentric refinements), the geodesics tend to be rather small. As for the boundary reflection. If a boundary is reached, we apply the geodesic law in the boundary and then apply the usual law. It is quite elegant because it works in arbitary dimensions. The code does not care about the dimension.
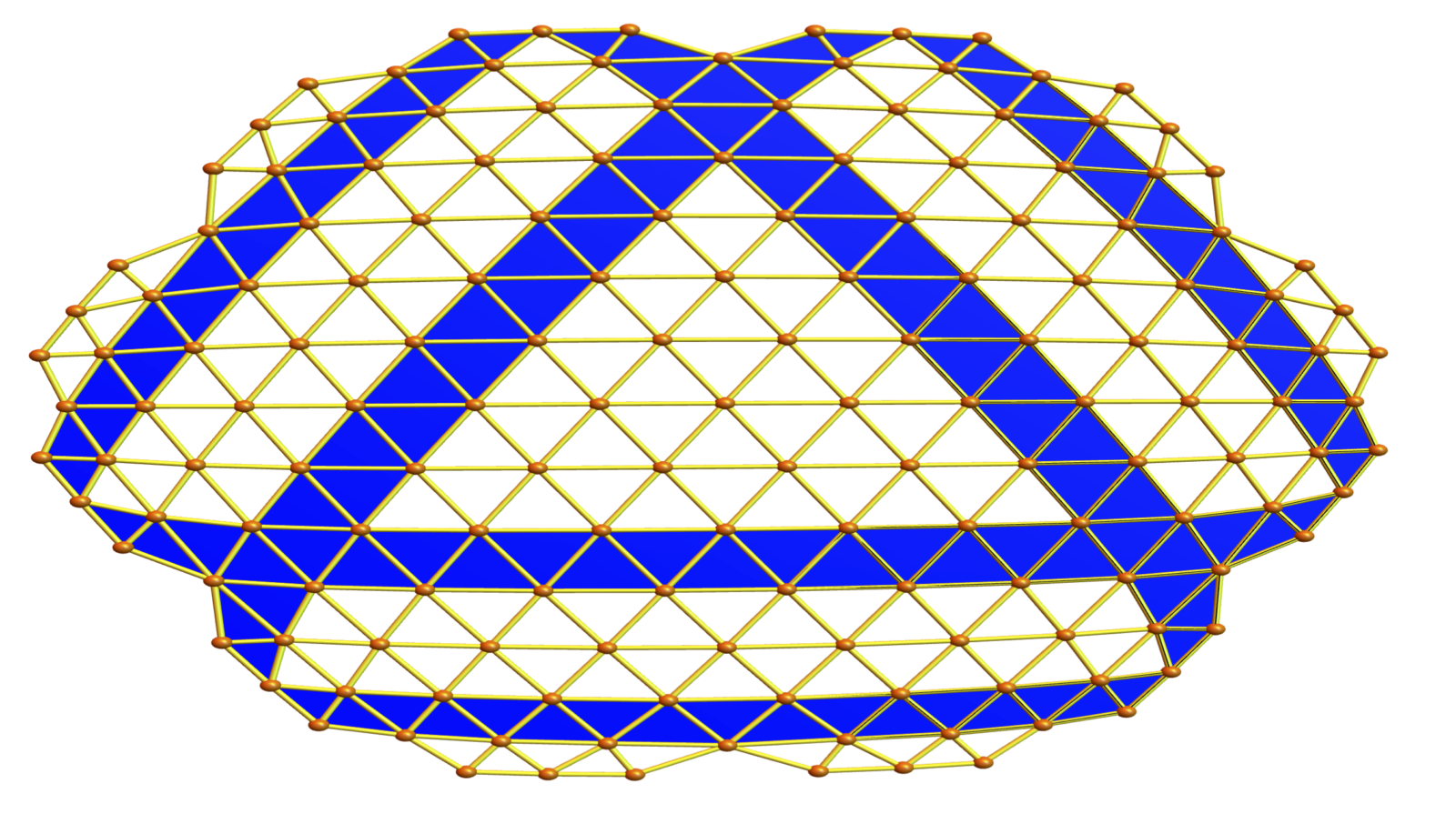
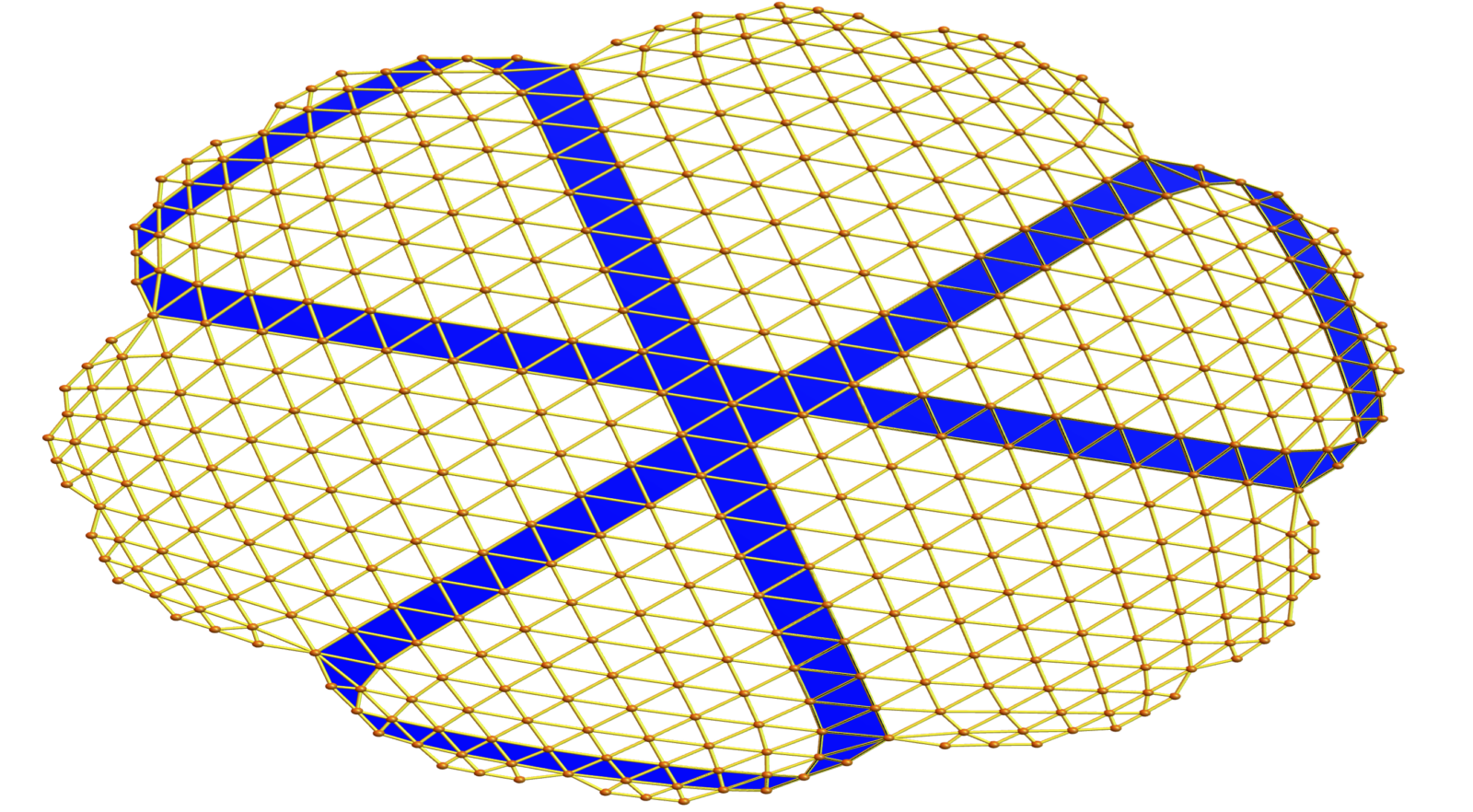
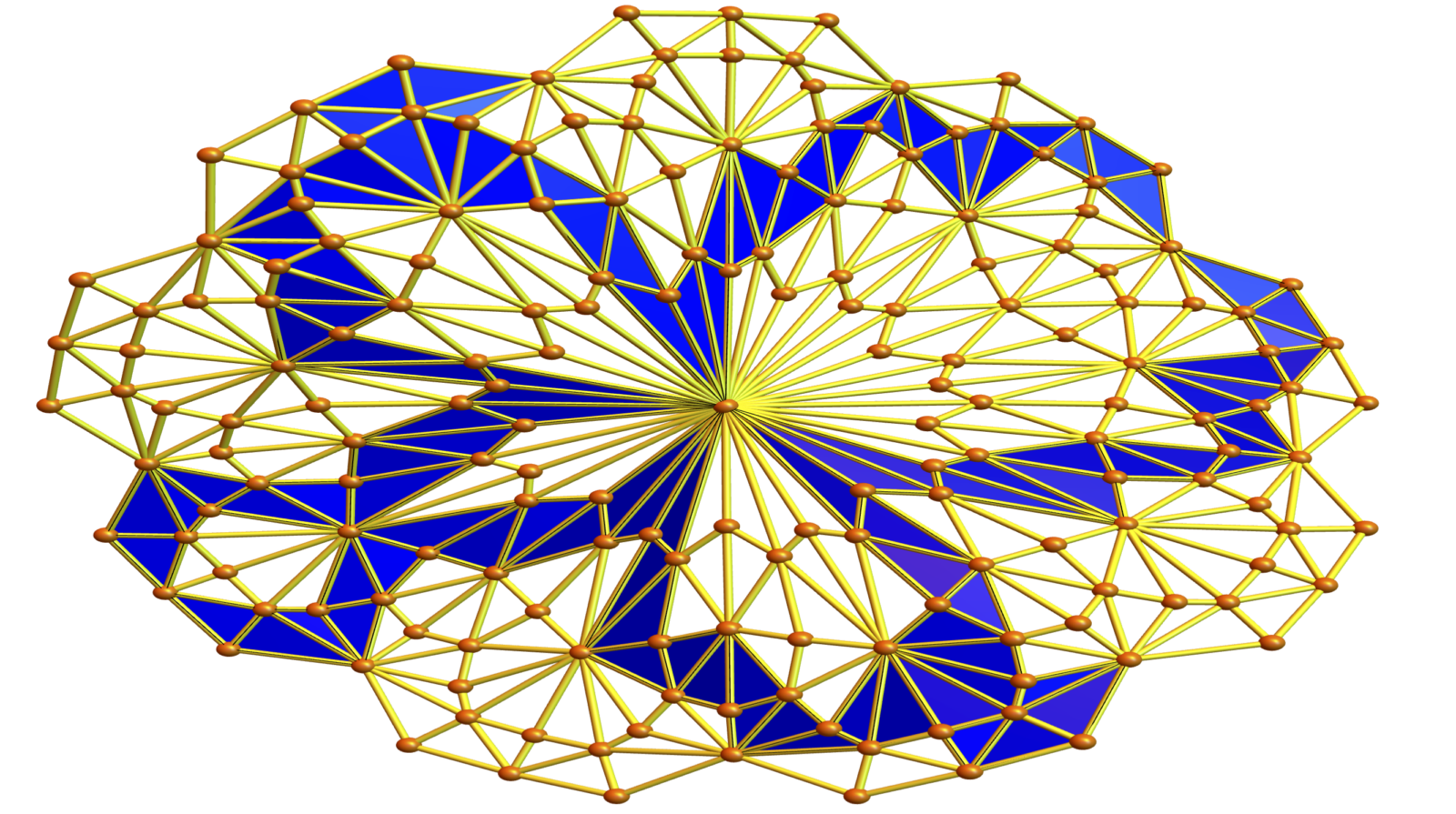
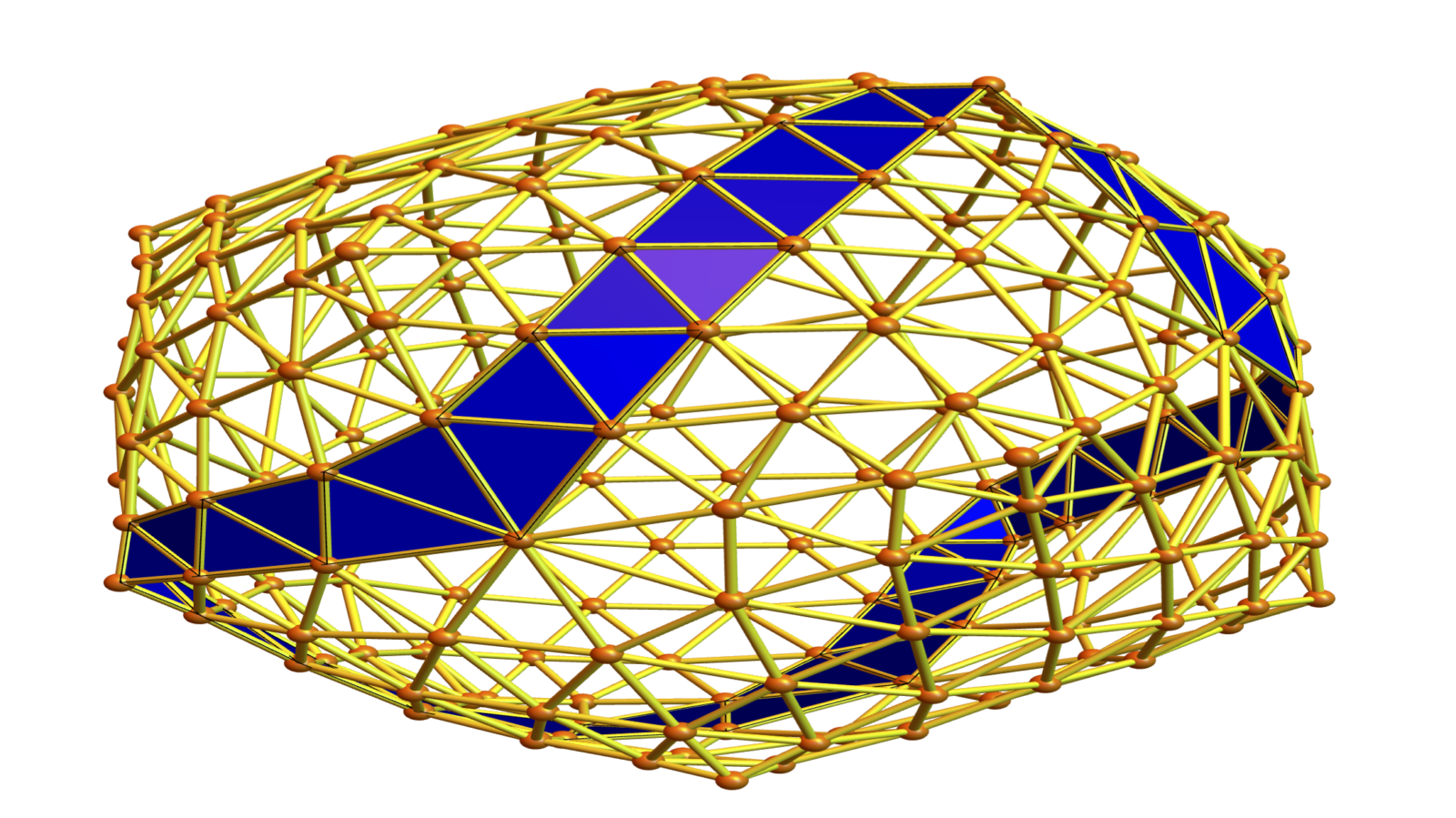
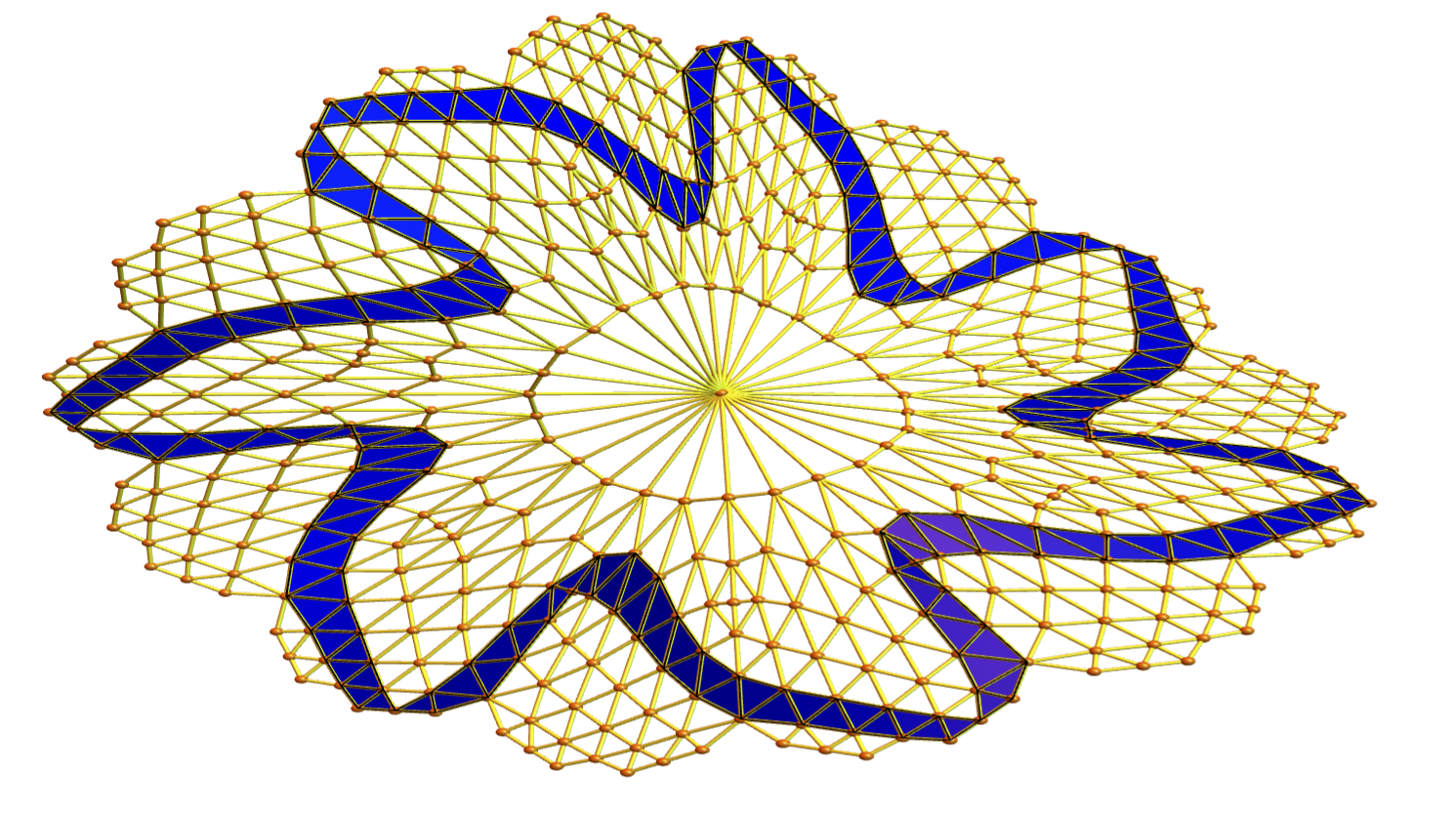
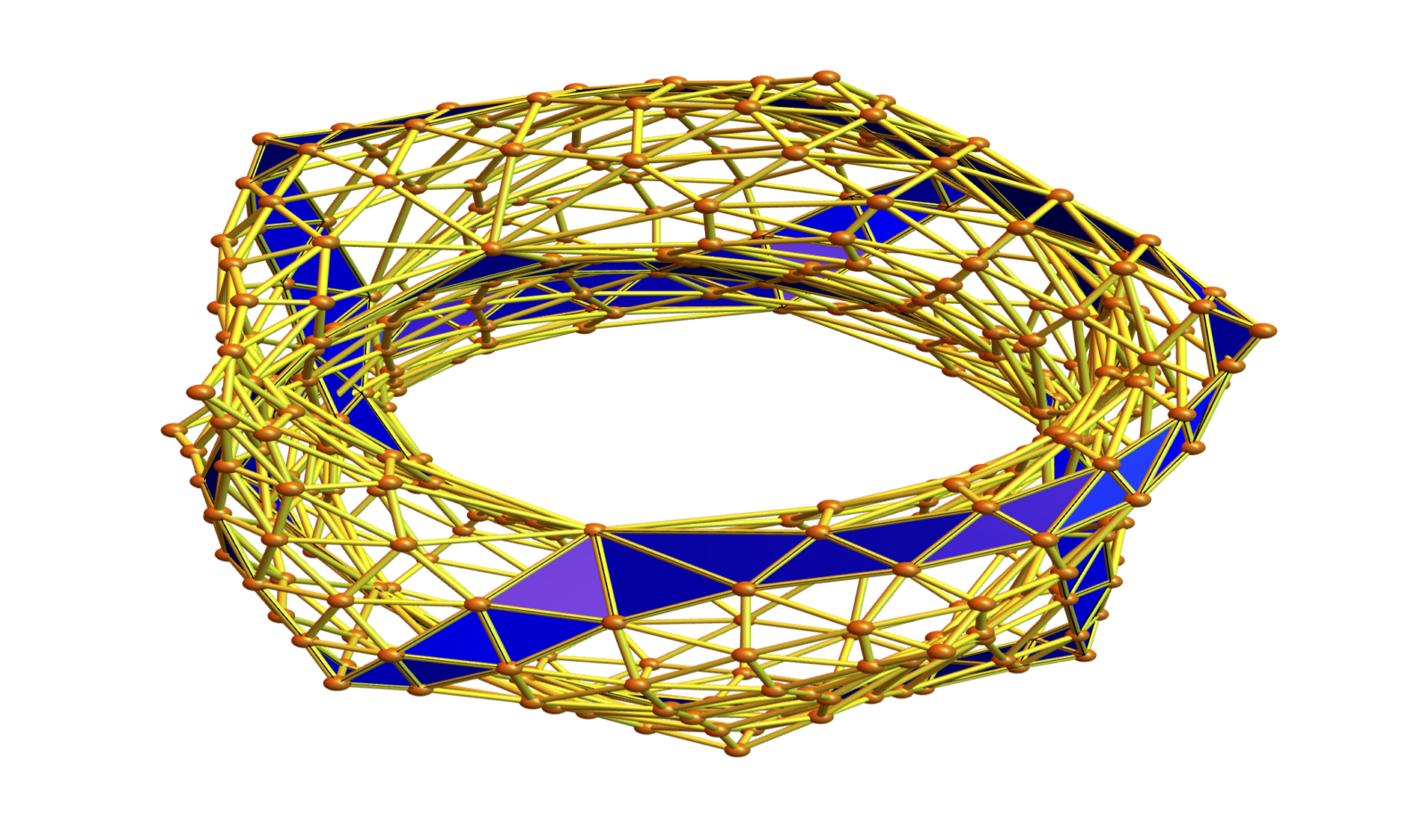
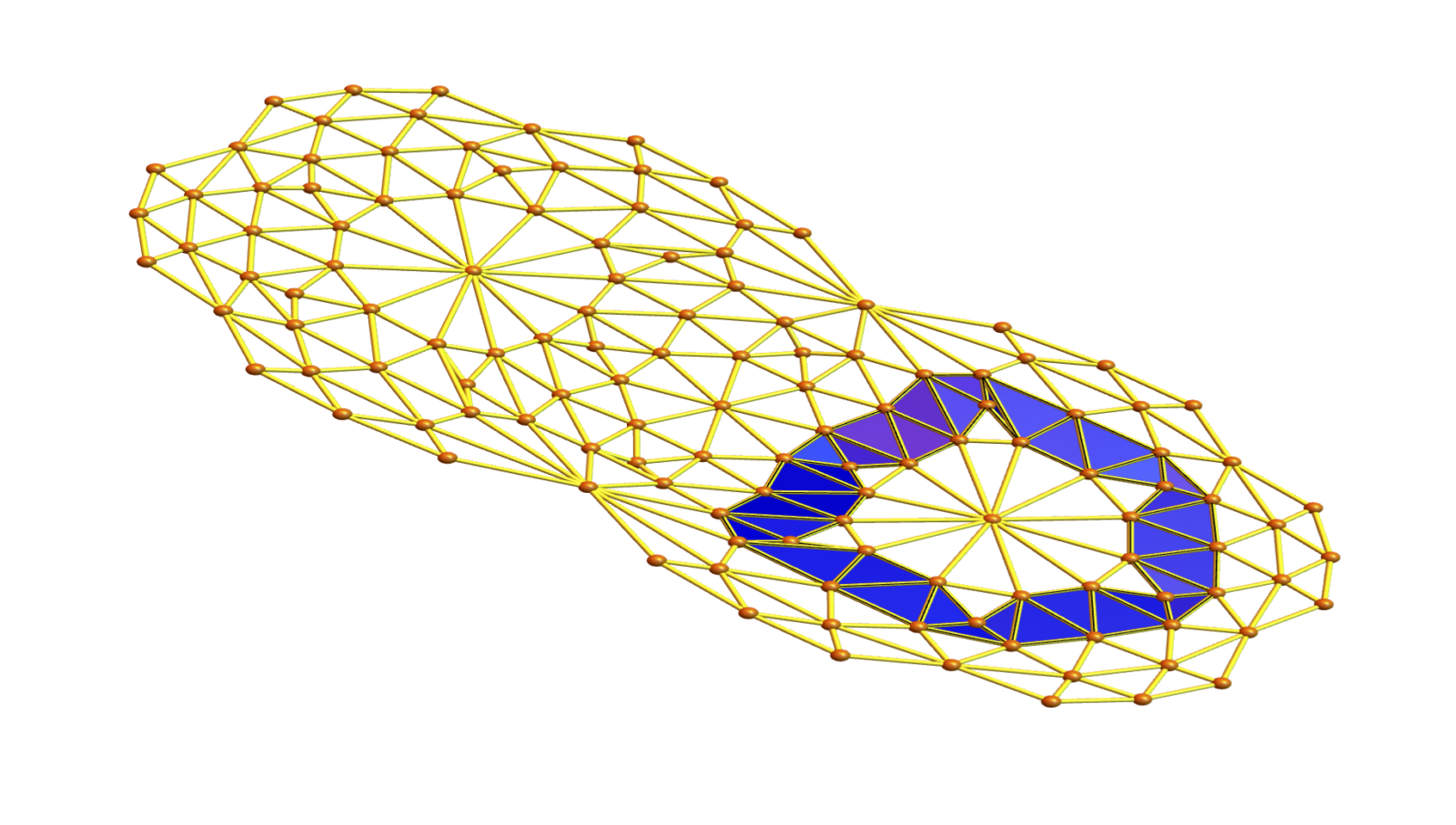


What is nicely fitting here is the form curvatures we have worked on last year. For any pure simplicial complex, we can in particular define a curvature on the maximal simplices such that the sum is the Euler characteristic. What is now remarkable is that geodesics can be characterized as chains of maximal simplicial complexes such that the curvature is constant zero (except at the boundary). If we take a cyclic polytop with more than 3 simplices hinging on a bone, then the curvature is not zero, there is a curve.
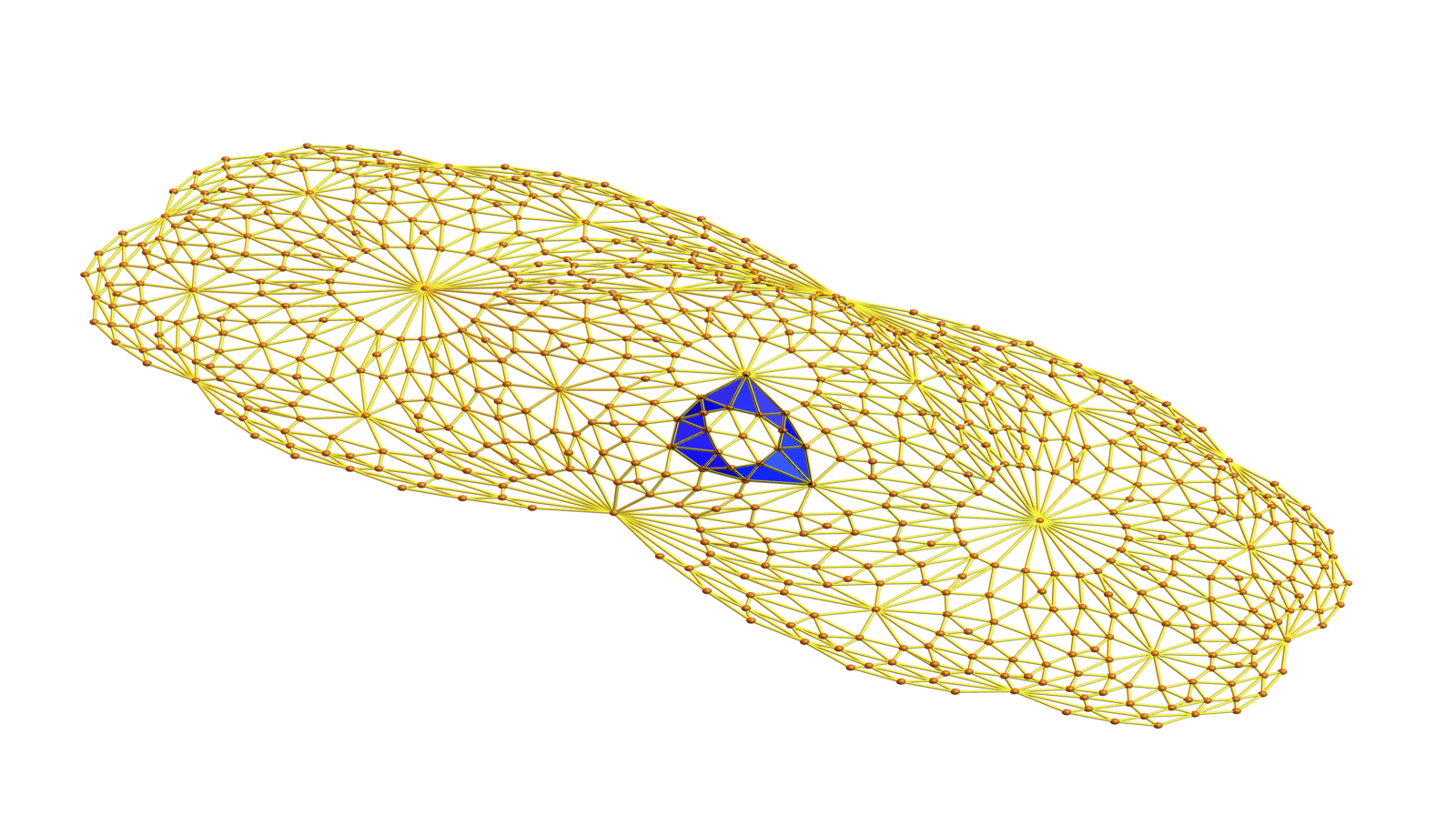
We can now give a definition of geodesic sheet. Take a bone which is a
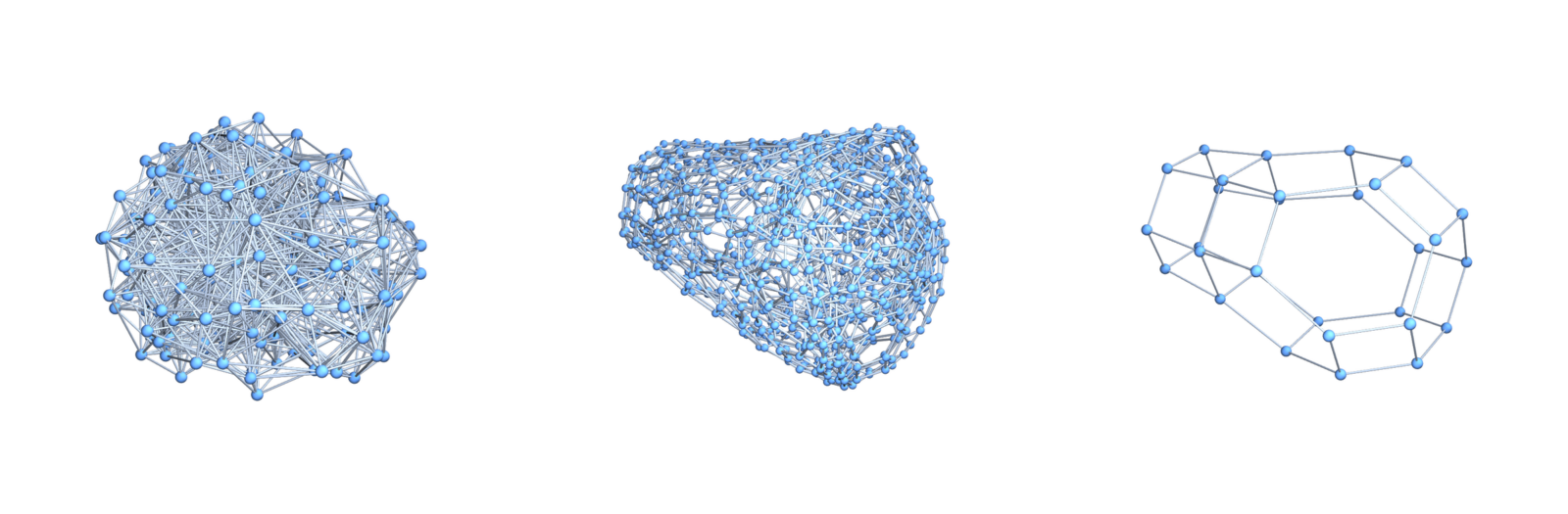
. Its dual sphere is a 1-sphere. This produces the first cell in the geodesic sheet. Now, use the geodesics starting at every facet in that cell to enlarge the cell complex one ring further. In order to get this sheet, we need to define orientations which produce us a sheet. For now, I just ordered the facets in such a way that the bone was at the beginning and keeps the same orientation. Then every simplex can come with maximal two orientation meaning that we just take two geodesics starting from each of the facets. Sometimes, they are the same. In the presentation I claimed that the cell complex we get by extending the bone building the seed of the sheet has as a dual a triangulated manifold. This is not necessarily the case. But it is naturally a 2 dimensional manifold. Here is an example. We see to the left the manifold G (which is in this case the real projective space
. In the middle we see its dual. To the right we see a sheet.