In the context of quantum calculus one is interested in discrete structures like graphs or finite abstract simplicial complexes studied primarily in combinatorics or combinatorial topology. Are they geometry? Are they calculus? What is geometry? In MathE320 I try to use the following definition: Geometry is the science of shape, …
The mathematics of evolving fields with two complex components is known already in Jones calculus.
This blog entry delivers an other example of an elliptic complex which can be used in discrete Atiyah-Singer or Atiyah-Bott type setups as examples. We had seen that when deforming an elliptic complex with an integrable Lax deformation, we get complex elliptic complexes. We had wondered in that blog entry …
As a follow-up note to the strong ring note, I tried between summer and fall semester to formulate a discrete Atiyah-Singer and Atiyah-Bott result for simplicial complexes. The classical theorems from the sixties are heavy, as they involve virtually every field of mathematics. By searching for analogues in the discrete, …
The strong ring is a category of geometric objects G which are disjoint unions of products of
simplicial complexes. Each has a Dirac operator D and a connection operator L. Both are related in
various ways to topology.
Implementing the Dirac operator D for products of simplicial complexes without going to the Barycentric refined simplicial complex has numerical advantages. If G is a finite abstract simplicial complex with n elements and H is a finite abstract simplicial complex with m elements, then is a strong ring element with …
In the book ‘This Idea Must Die: Scientific Theories That Are Blocking Progress’, there are two entries which caught my eye because they both belong to interests of mine: geometry and calculus. The two articles are provided below. [I believe it is “fair use” as a reprint of these two …
The strong ring The strong ring generated by simplicial complexes produces a category of geometric objects which carries a ring structure. Each element in the strong ring is a “geometric space” carrying cohomology (simplicial, and more general interaction cohomologies) and has nice spectral properties (like McKean Singer) and a “counting …
Elements in the strong ring within the Stanley-Reisner ring still can be seen as geometric objects for which mathematical theorems known in topology hold. But there is also arithemetic. We remark that the multiplicative primes in the ring are the simplicial complexes. The Sabidussi theorem imlies that additive primes (particles) have a unique prime factorization (into elementary particles).
The graph limit We can prove now that the graph limit of the connection graph of Ln x Ln which is the strong product of Ln‘ with itself has a mass gap in the limit n to infinity. The picture below shows this product graph for n=13, and to the …
Arithmetic with networks The paper “On the arithmetic of graphs” is posted. (An updated PDF). The paper is far from polished, the document already started to become more convoluted as more and more results were coming in. There had been some disappointment early June when realizing that the Zykov multiplication …
Depending on scale, there are three different Kepler problems: the Hydrogen atom, the Newtonian Kepler problem as well as the binary Blackhole problem. The question whether there is a unifying model which covers all of them is part of the quest of finding a quantum theory of gravity.
The dual multiplication of the ring of networks is topological interesting as Kuenneth holds for this multiplication and Euler characteristic is a ring homomorphism from this dual ring to the ring of integers.
We give two proofs that the additive Zykov monoid on the category of finite simple graphs has unique prime factorization. We can determine quickly whether a graph is prime and also produce its prime factorization.
The Hardy-Littlewood race has been running now for more than a year on my machine. The Pari code is so short that it is even tweetable. Here are some slides which also mention Gaussian Goldbach: What do primes have to do with quantum calculus? First of all, analytic number theory …
Motivated by the Hamiltonian of the Hydrogen atom, we can look at an anlogue operator for finite geometries and study the spectrum. There is an open conjecture about the trace of this operator.
Update of May 27, 2017: I dug out some older unpublished slides authored in 2015 and early 2016. I added something about the quantum gap and something on the quantum plane at the very end. Here is the presentation, just spoken now. The quantum line In one dimension, there is …
The Barycentric limit of the density of states of the connection Laplacian has a mass gap.
The tensor product is defined both for geometric objects as well as for morphisms between geometric objects. It appears naturally in connection calculus.
We look at examples of functional integrals on finite geometries.
As Goedel has shown, mathematics can not tame the danger that some inconsistency develops within the system. One can build bunkers but never will be safe. But the danger is not as big as history has shown. Any crisis which developed has been very fruitful and led to new mathematics. (Zeno paradox->calculus, Epimenids paradox ->Goedel, irrationality crisis ->number fields etc.
As we have an internal energy for simplicial complexes and more generally for every element in the Grothendieck ring of CW complexes we can run a Hamiltonian system on each geometry. The Hamiltonian is the Helmholtz free energy of a quantum wave.
Energy theorem The energy theorem tells that given a finite abstract simplicial complex G, the connection Laplacian defined by L(x,y)=1 if x and y intersect and L(x,y)=0 else has an inverse g for which the total energy is equal to the Euler characteristic with . The determinant of is the …
The history of the developent of energy and entropy is illustrated. This page is a picture book featuring some of the people involved shaping the concept of energy.
Over spring break, the Helmholtz paper [PDF] has finished. (Posted now on “On Helmholtz free energy for finite abstract simplicial complexes”.) As I will have little time during the rest of the semester, it got thrown out now. It is an interesting story, relating to one of the greatest scientist, …
Energy U and Entropy S are fundamental functionals on a simplicial complex equipped with a probability measure. Gibbs free energy U-S combines them and should lead to interesting minima.
Entropy is the most important functional in probability theory, Euler characteristic is the most important functional in topology. Similarly as the twins Apollo and Artemis displayed above they are closely related. Introduction This blog mentions some intriguing analogies between entropy and combinatorial notions. One can push the analogy in an …
An experimental observation : the sum over all Green function values is the Euler characteristic. There seems to be a Gauss-Bonnet connection.
The sphere spectrum paper is submitted to the ArXiv. A local copy. It is an addition to the unimodularity theorem and solves part of the riddle about the Green function values, the diagonal elements of the inverse of the matrix 1+A’ where A’ is the adjacency matrix of the connection …
What happens with the spectrum of the Laplacian if we add some graphs or simplicial complexes? (I owe this question to An Huang). Here is an example, where we sum a circular graph G=C4 and a star graph H=S4. The Laplace spectrum of G is {4,2,2,0}, the spectrum of H …
Assuming the join operation to be the addition, we found a multiplication which produces a ring of oriented networks. We have a commutative ring in which the empty graph is the zero element and the one point graph is the one element. This ring contains the usual integers as a subring. In the form of positive and negative complete subgraphs.
The join operation on graphs produces a monoid on which one can ask whether there exists an analogue of the fundamental theorem of arithmetic. The join operation mirrors the corresponding join operation in the continuum. It leaves spheres invariant. We prove the existence of infinitely many primes in each dimension and also establish Euclid’s lemma, the existence of prime factorizations. An important open question is whether there is a fundamental theorem of arithmetic for graphs.
This is a research in progress note while finding a proof of a conjecture formulated in the unimodularity theorem paper.
During the summer and fall of 2016, Annie Rak did some URAF (a program formerly called HCRP) on partial differential equations on graphs. It led to a senior thesis in the applied mathematics department. Here is a project page and here [PDF] were some notes from the summer. The research …
Here are some slides about the paper. By the way, an appendix of the paper contains all the code for experimenting with the structures. To copy paste the code, one has to wait for the ArXiv version, where the LaTeX source is always included. Here is the unimodularity theorem again …
The Christmas Theorem Because Pierre de Fermat announced his two square theorem to Marin Mersenne in a letter of December 25, 1640 (today exactly 376 years ago) the theorem A prime of the form 4k+1 is the sum of two squares. is also called the Christmas theorem. The converse, the …
This is an informal overview over definitions of dimension, both in the continuum as well as in the discrete. It also contains suggestions for generalizations to general metric spaces.
The following picture illustrates the Euler and Fredholm theme in the special case of the prime graphs introduced in the Counting and Cohomology paper. The story there only dealt with the Euler characteristic, an additive valuation (in the sense of Klain and Rota). Since then, the work on the Fredholm …
The unimodularity theorem equates a fredholm determinant with a product of indices. It originally was formulated for graphs or simplicial complexes. It turns out to be valid for more general structures, generalized cellular complexes. While for discrete CW complexes, the fredholm determinant is 1 or -1, in general it can now take more general values but the structures are also more strange: in the continuum much more general than CW complexes as the attached cells do not need to be bound by spheres but can be rather arbitrary.
Just uploaded a larger version of my 2013 Pecha-Kucha talk “If Archimedes knew functions…”. The Pecha-Kucha format of presenting 20 slides with 20 seconds time each is fantastic to keep talks concise and to the point. The video has been produced by Diane Andonica from the Bok Center for teaching …
Zeta functions are ubiquitous in mathematics. One of the many zeta functions, the Bowen-Lanford Zeta function was introduced by my Phd dad Oscar Lanford and Rufus Bowen. I am in the process to wrap up a proof of a theorem which is so short that its statement can be done …
Paul Kustaanheimo (1924-1997) was a Finnish astronomer and mathematician. In celestial mechanics, his name is associated with the Kustaanheimo-Stiefel transform or shortly KS transform which allows to regularize the Kepler problem using Clifford algebras. In this elegant picture, the motion of the two bodies becomes a rotation in three dimensions …
Source: Pride and Prejudice, 2005 Judy Dench plays the role of Lady Catherine de Bourgh. I recently posted a “Particles and Primes” as well as a “Counting and Cohomology” article on the ArXiv, because, as it is a truth universally acknowledged, that an article in possession of a good result, …
There are various cohomologies for finite simplicial complexes. If the complex is the Whitney complex of a finite simple graph then many major results from Riemannian manifolds have discrete analogues. Simplicial cohomology has been constructed by Poincaré already for simplicial complexes. Since the Barycentric refinement of any abstract finite simplicial complex is always the Whitney complex of a finite simple graph, there is no loss of generality to study graphs instead of abstract simplicial complexes. This has many advantages, one of them is that graphs are intuitive, an other is that the data structure of graphs exists already in all higher order programming languages. A few lines of computer algebra system allow so to compute all cohomology groups. The matrices involved can however become large, so that alternative cohomologies are desired.
The standard model of particle physics is not so pretty, but it is successful. Many lose ends and major big questions remain: is there a grand unified gauge group? Why are there three generations of particles? Why do neutrini oscillate? How is general relativity included? (See for example page 540 …
Traditional calculus often mixes up different spaces, mostly due to pedagogical reasons. Its a bit like function overload in programming but there is a prize to be payed and this includes confusions when doing things in the discrete. Here are some examples: while in linear algebra we consider row and …
[Update, March 20, 2018: see the ArXiv text. See also an update blog entry with some Mathematica code. More mathematica code can be obtained from the TeX Source of the ArXiv article.]. Classical calculus we teach in single and multi variable calculus courses has an elegant analogue on finite simple …
Update: March 8, 2016: Handout for a mathtable talk on Wu characteristic. Gauss-Bonnet for multi-linear valuations deals with a number in discrete geometry. But since the number satisfies formulas which in the continuum need differential calculus, like curvature, the results can be seen in the light of quantum calculus. Here …
A finite graph has a natural Barycentric limiting space which can serve as the geometry on which to do quantum calculus or physics. The holographic picture has universal spectral properties.
How to define level surfaces or solve extremization problems in a graph. A comment on a recent paper on Sard.
Quantum calculus is easy to learn, allows experimentation with small worlds and allows to use the same notation we are used to classically.
Calculus on graphs is a natural coordinate free frame work for discrete calculus.
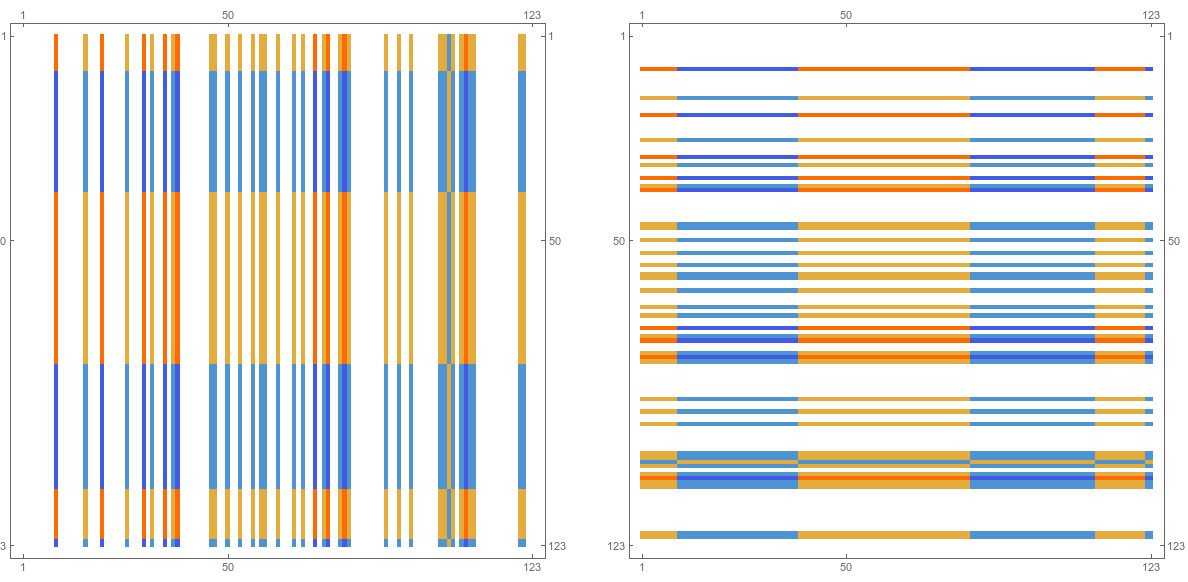
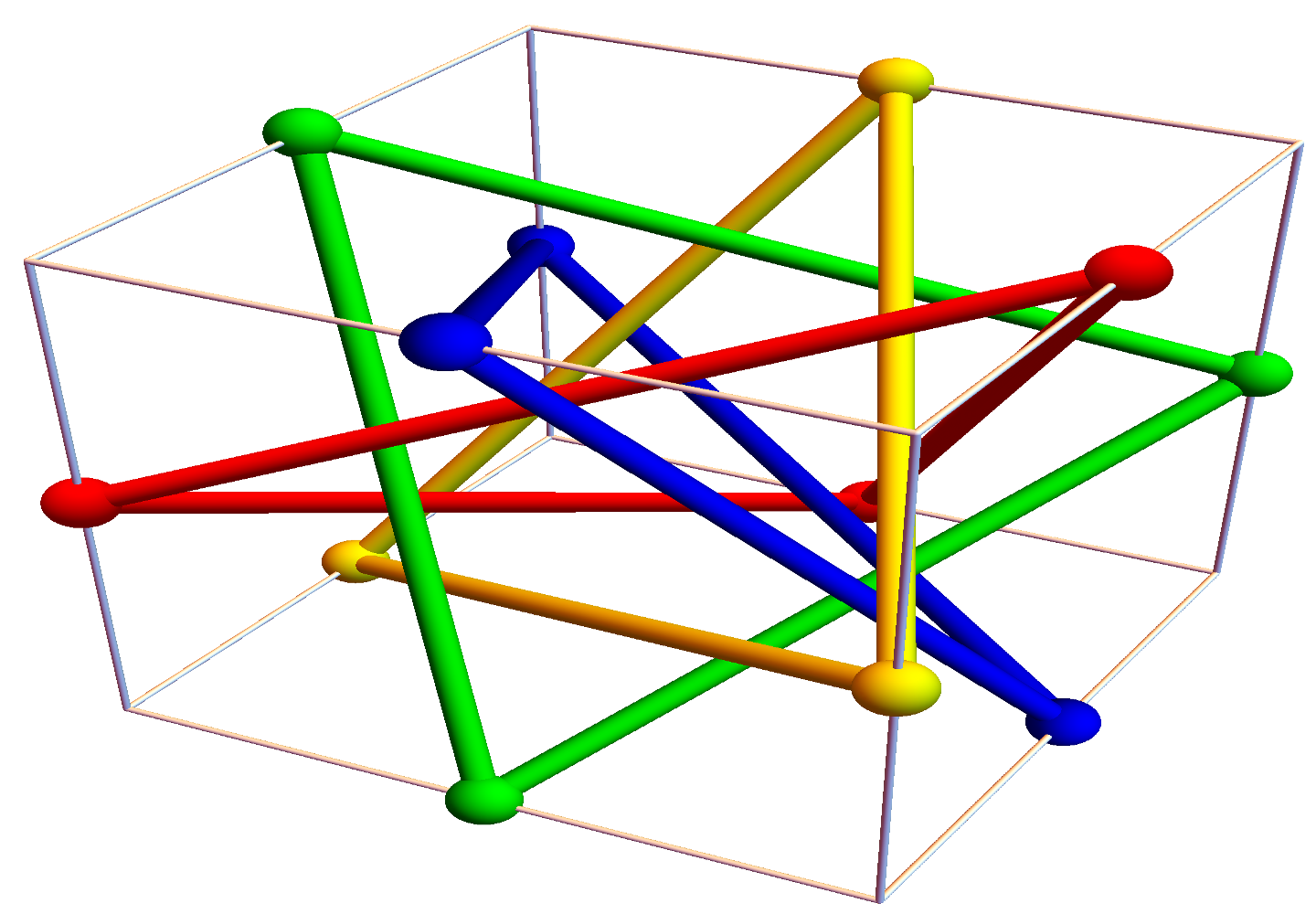
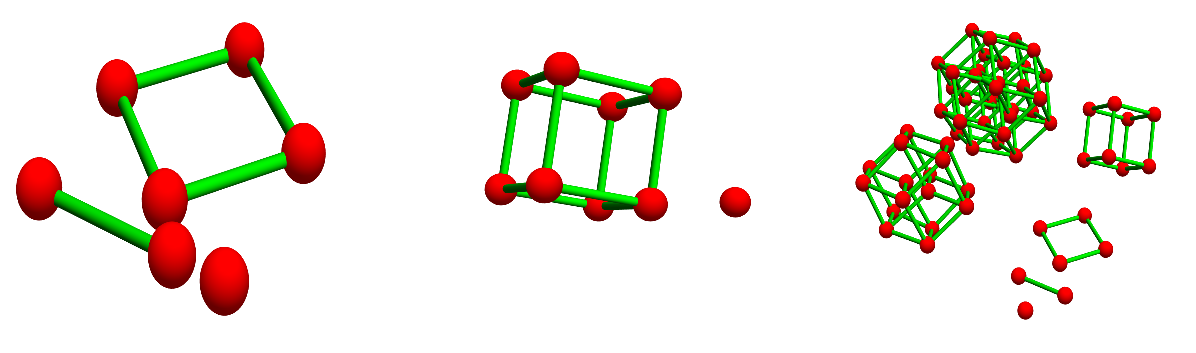
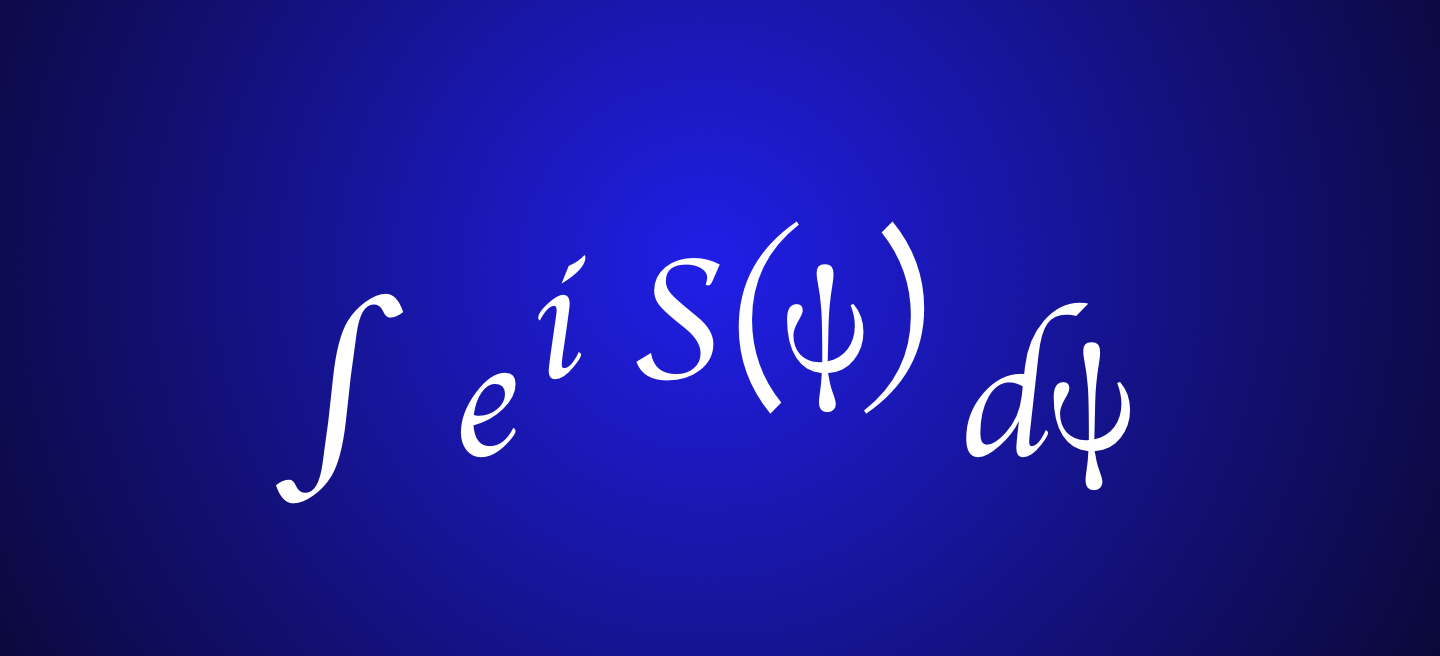We have seen that 
![D[x]^n = n [x]^{n-1}](https://s0.wp.com/latex.php?latex=D%5Bx%5D%5En+%3D+n+%5Bx%5D%5E%7Bn-1%7D&bg=ffffff&fg=000000&s=0 "D[x]^n = n [x]^{n-1}")
We will often leave the constant $h$ out of the notation and use terminology like 
![[x]^n](https://s0.wp.com/latex.php?latex=%5Bx%5D%5En&bg=ffffff&fg=000000&s=0 "[x]^n")
Define the exponential function as
![exp(x) = \sum_{k=0}^{\infty} [x]^k/k!](https://s0.wp.com/latex.php?latex=exp%28x%29+%3D+%5Csum_%7Bk%3D0%7D%5E%7B%5Cinfty%7D+%5Bx%5D%5Ek%2Fk%21&bg=ffffff&fg=000000&s=0 "exp(x) = \sum_{k=0}^{\infty} [x]^k/k!")
![exp_n(x) = \sum_{k=0}^{n} [x]^k/k!](https://s0.wp.com/latex.php?latex=exp_n%28x%29+%3D+%5Csum_%7Bk%3D0%7D%5E%7Bn%7D+%5Bx%5D%5Ek%2Fk%21&bg=ffffff&fg=000000&s=0 "exp_n(x) = \sum_{k=0}^{n} [x]^k/k!")
where $e_n \to e$. Because $n \to e_n$ is monotone, we see that the exponential function 
Since the just defined exponential function is monotone, it can be inverted on the positive real axes. Its inverse is called 
Let denote the discrete derivative of a continuous function f on the real line. In this post, I assume that all functions are continuous of have compact support. They are zero outside some large interval. No smoothness is required of course. Here is the simplest version of the fundamental theorem …
Assume f is a continuous function of one real variable. Lets call a point p a critical point of f if Df(p)=0 where Df(x) = f(x+1)-f(x) is the discrete derivative of f. As in classical calculus, a point p is called a local maximum of f, if there exists an …
