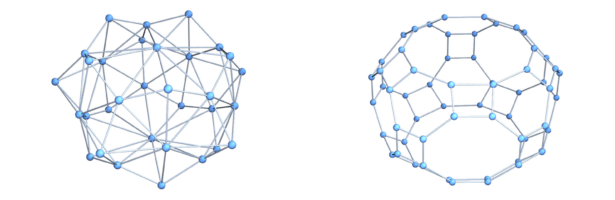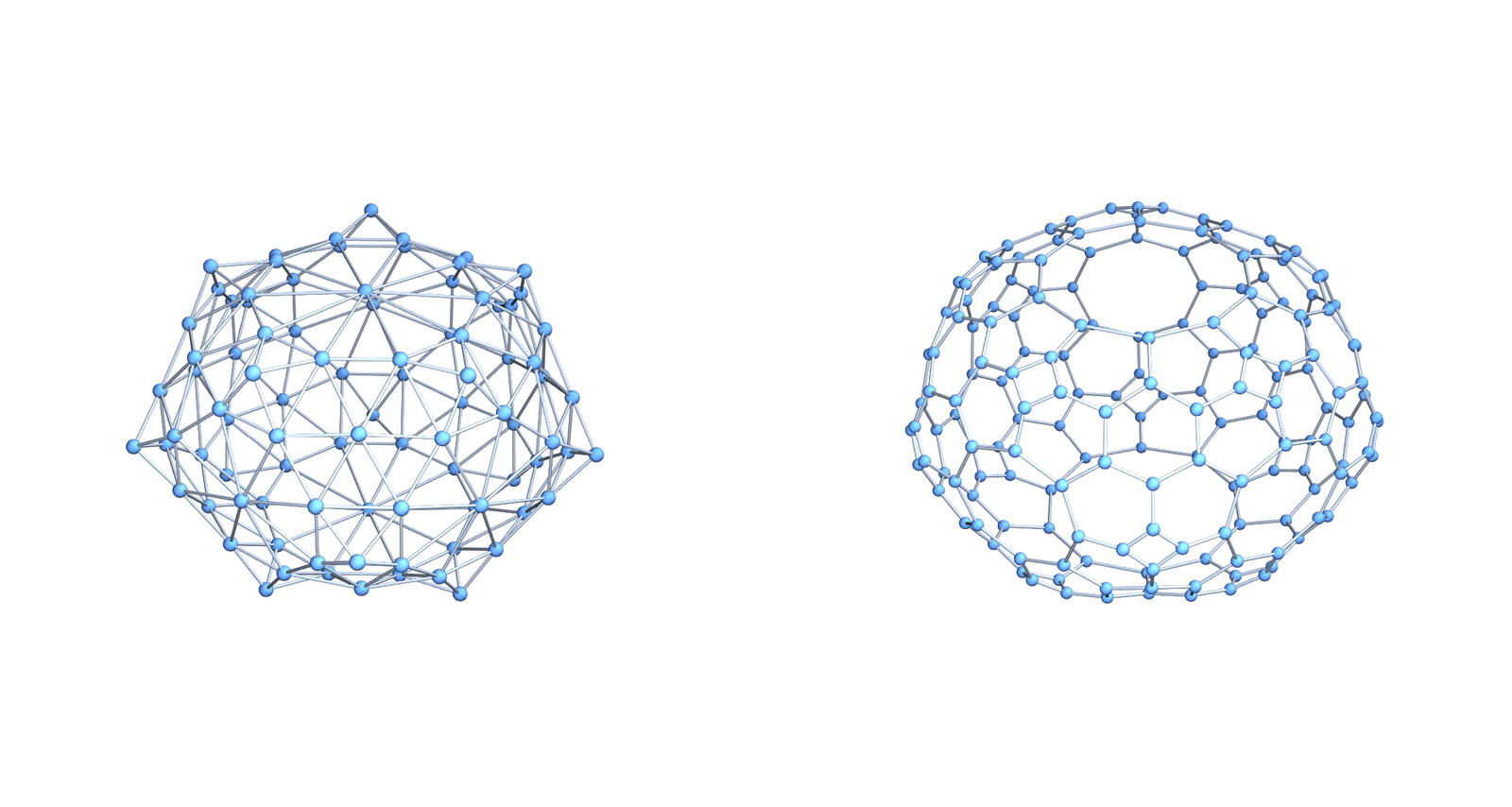
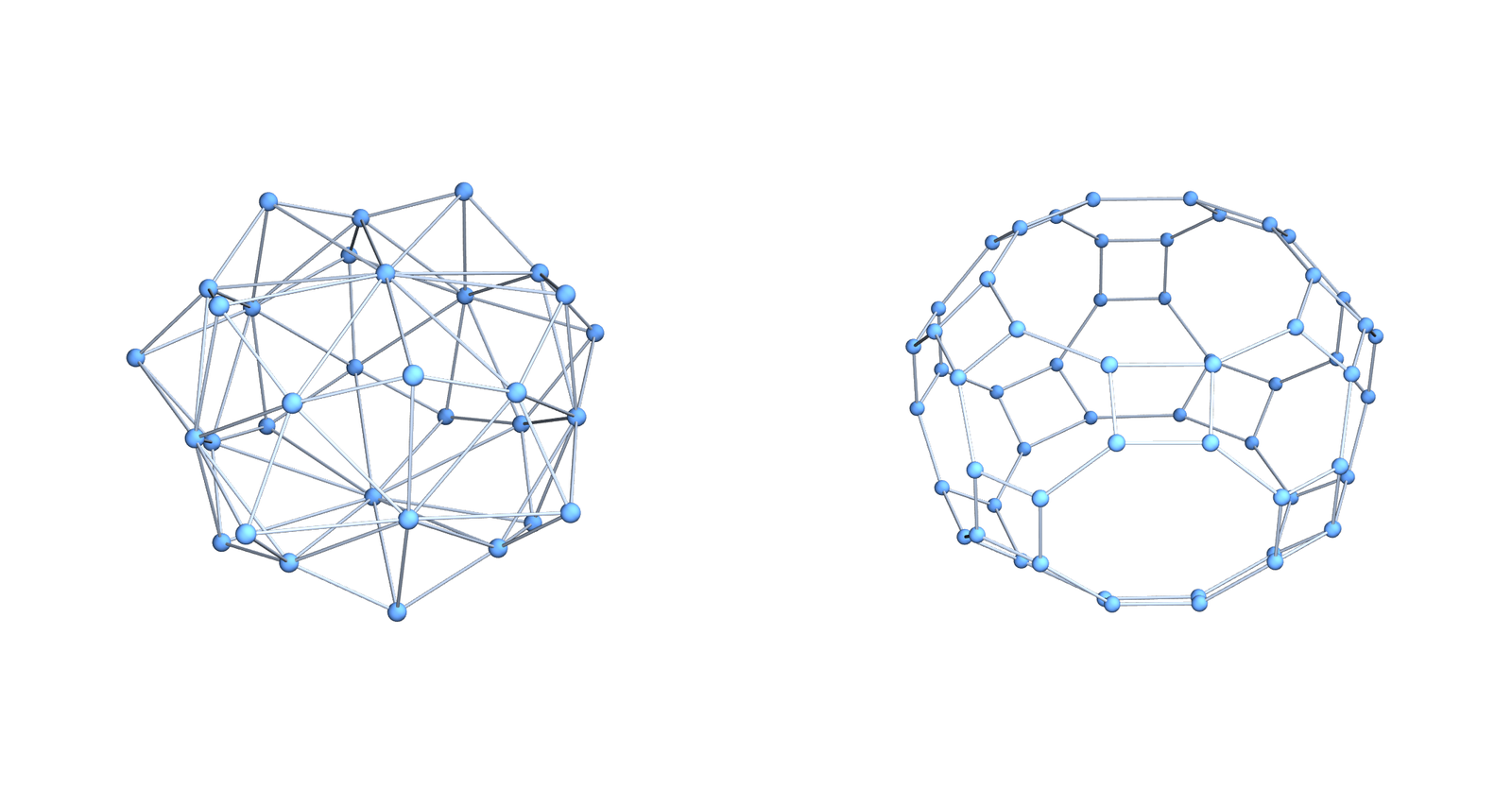
Coloring manifolds is a wonderful theme because it is not that well studied and so has many low hanging fruits. Here is an other one. For d-manifolds, the chromatic number is between d+1 and 2d+2 and a growth rate (3d+1)/2 is observed and reasonably conjectured upper bound. I started to work on this in 2014 https://arxiv.org/abs/1412.6985 and then worked more on it in 2021 https://arxiv.org/abs/2106.14374. (See also this youtube video from June 2021 and this youtube video from 2014, now exactly 10 years ago. ) What plays an important role here is the dual graph, which has maximal simplices as vertices and connect two if they intersect in a d-1 dimensional simplex. These dual graphs have no triangles and their coloring properties matter when looking at the chromatic number of soft Barycentric refined manifolds. To the right, we see first an example of a 2-sphere and its dual graph. What is nice about these dual graphs is that their vertex arboricity is 2 and that they can be colored by 2 or 3 colors. The first fact immediately leads to the bound 2d+2 and the second leads to the statement that soft Barycentric refined d- manifolds have chromatic number d+1 or d+2. Barycentric refined manifolds of course have always chromatic number d+1 because the dimension is a coloring. The picture above then shows the soft Barycentric refinement and its dual graph.