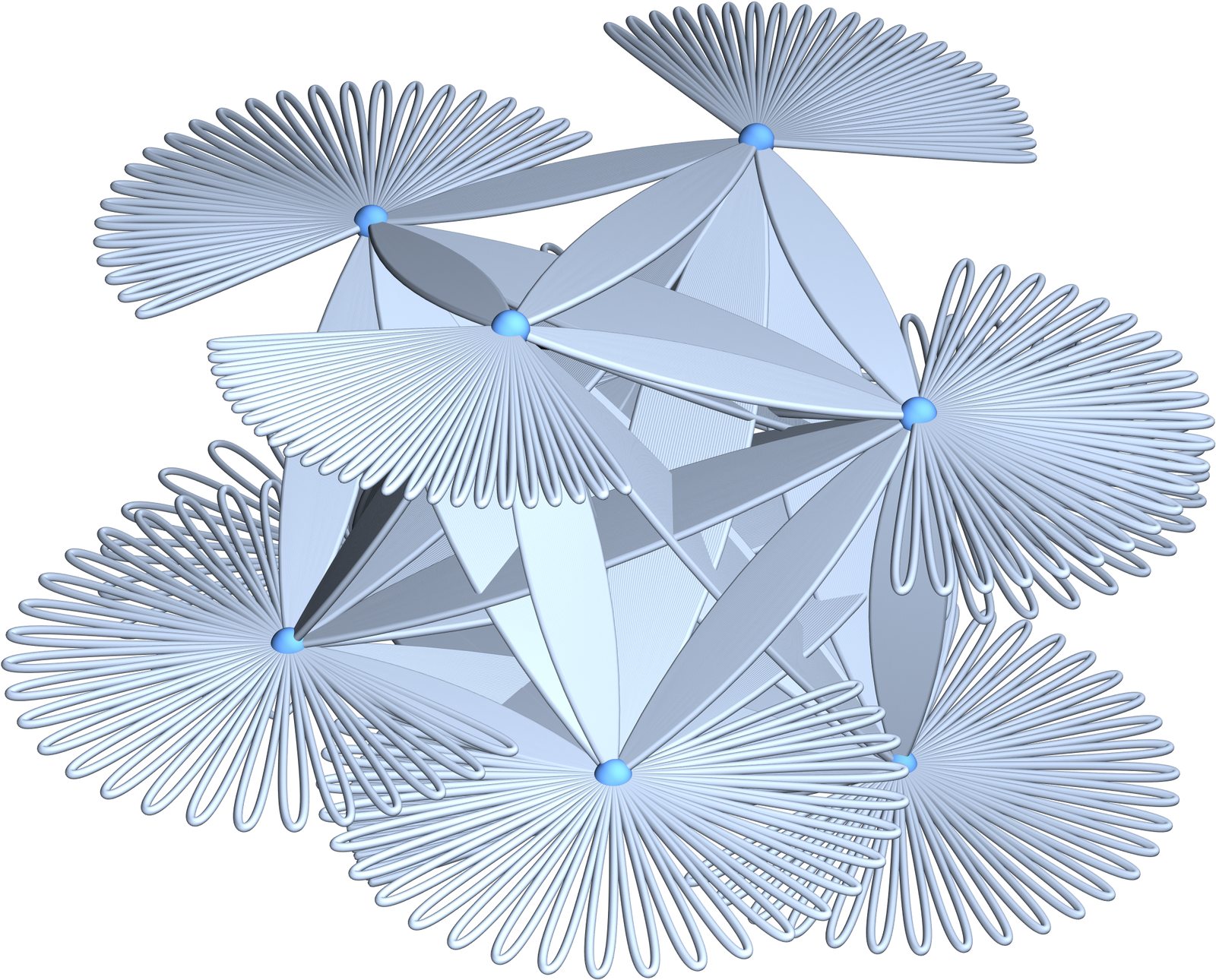
Quivers are graph in which multiple connections and loops are allowed. Since there is a Dirac operator d+d* with exterior derivative for them, they define a one-dimensional delta set (G,D,r), where G is the union of vertices and edges (loops count as edges) and r is the dimension function which is zero for vertices and 1 for loops and connections. For finite simple graphs, there is a natural Whitney functor getting from the graph to a d-dimensional simplicial complex, where d is the dimension of the maximal complete subgraph. This is the Whitney complex, the 1 dimensional topologists complex as in the early 20th century, the skeleton of a triangulation of a manifold is a graph and not the graph theorists complex V union E. The one dimensional complex is rather limiting (it is of course still useful as any skeleton complex, but it is a skeleton, does not have meat!) . Here is an updated paper [PDF] about the eigenvalue bounds for the Kirchhoff Laplacian of a quiver. It now also includes Mathematica code, more references, pictures were updated and in general, everything is smoothed out a bit. Look at the following 1-line code GraphPlot3D[Graph[Table[Random[Integer, 10] -> Random[Integer, 10], {3000}]]] for example. It generates a random quiver with 10 vertices and 3000 edges. Note that loops are counted as edges so that the Euler characteristic of this quiver is 10-3000=-2990. This is the Euler characteristic of the quiver to the left. The topic of the course was actually whether there is a natural functor from the topos of quivers to the topos of 1-dimensional delta sets (which is obvious) but that I suspect that there is a natural more general functor which extends the Whitney functor, that maps a finite simple graph to a finite abstract simplicial complex with the topologists dimension (clique number -1) and not just the graph theorists dimension (the boring 1). Back to the one liner producing a random quiver with 10 vertices and 3000 edges: GraphPlot3D[Graph[Table[Random[Integer, 10] -> Random[Integer, 10], {3000}]]] with a possible picture is seen to the right. In the case of graph, we can reformulate this and specify the probability p that any of the n(n+1)/2 edges of a complete is turned on. Since the number of vertices and edges can be chosen quite independently for quivers, an Erdoes-Renyi space would be a space where the number of edges is chosen with some natural distribution like the geometric distribution (the distribution which maximizes entropy on the natural numbers and is so the most natural distribution!) The probably to have m edges is then which is a discrete probability distribution.

[Let me add a (rather personal) remark about the upper bound theorem which is valid for all eigenvalues and all quivers. Also after two years, I’m still very pleased with the theorem. It is a general theorem because it is a theorem that hold for all elements in an entire category. [To be fancy, actually for an entire topos (finite quivers can be seen as a pre-sheave category
, where
is the opposite category of the Kronecker quiver)]. Furthermore, like any result in spectral theory, it relates a topological notion (the vertex degrees) with an algebraic notion, the eigenvalues. Spectral theory adds an analytic touch to the topological frame work of quivers are linked to algebra. So, it is not just a theorem about a specific object or narrow class of objects it is a theorem valid for a category. When I was a teenager and started to become interested in mathematics, I dreamed about finding and proving a theorem on my own. That would be my life goal. I think having achieved that (By the way, I also think it is important how a result is obtained. I pride myself of having done this on my own, not with any coauthor. It is like climbing free solo rather than in a team. Of course, also climbing in teams is fun and actually more relaxing as it is safer, but “free solo” is the ultimate challenge, where every single move is done on your own without help, also not from AI.) While graduating from college, I became more (too) ambitious and from 1987 to 2000, I pursued an open problem in ergodic theory which is still open today, the problem of positive entropy of the standard map. It was a climb which ended up in a crash. In science it is brutal. ( If you do not get tenure until 30 the game is over, its the analog of falling badly during a climb so the temptation is big to risk a lot, I wrote about risk once in a letter to the class of 2021. This was during the time of the pandemic where estimating risk was a major issue). This entropy problem actually is very much related also to the spectral problem of quivers. The problem of positive metric entropy for the standard map is the problem to prove that the potential
is positive for z=0, where a density of states measure
is given by a discrete random Schroedinger operator. It is the Hessian of the variational principle defining the system, these are discrete Lagrange or discrete Hamiltonian systems with variational descriptions. Random operator is understood in the sense of random variable: it is an operator valued random variable. This does not mean the underlying system shows any randomness. The famous almost Matthieu operator is an example of a random operator, where the probability space is the circle and the potential values (classical random variables) are obtained along a group translation on that torus. Quivers, when defined over a circular graph , define Jacobi matrices. I explain in the paper that having a priori only integer potential values is not a problem as we can scale and shift the operator and so the spectrum. Giving estimates for all eigenvalues for such matrices is a big deal in mathematical physics and can make an impact for estimating the potential U(z) which is in the operator theory or chaos theory jargon is called the Lyapunov exponent, a subharmonic function. In the context of graphs, one has the rooted tree number
which is the pseudo determinant of the Laplacian. If we take the log we get
, which is the potential
for a point measure
. So, with this work, I got again close to a problem, I had been pursuing for along time, also with potential theoretical attempts. It would have been really nice to prove the problem about positive entropy of the standard map, but if we look at it with a rational head, it is one particular dynamical system, it might lead to results for more general systems but still, it would be rather limited to a narrow class of dynamical systems. The upper bound theorem however is a very general theorem for an entire category and so much more valuable when seen from a neutral perspective. The valuation of problem however is social: the result had not been a conjecture from 60 years ago like the positive entropy problem for the standard map. The quiver theorem just appeared while trying to estimate the tail distribution of the Barycentric limit measure. Additionally, the proof is not difficult, consisting essentially just of induction and the interlace theorem. It relates to the entropy problem of the standard map matheamtically but unfortunately, it does not produce strong enough results to estimate the density of states of random Schroedinger operators. For estimating the Lyapunov exponents for energies inside the spectrum, one problem is that for pure point measures, the logarithmic potential gets unbounded at the spectrum. (estimating the entropy outside the spectrum, where one has a hyperbolic behavior is easy. The entropy is positive simply because a subharmonic function (with logarithmic growht) has potential larger than 0 outside the Riesz measure. We really need to look at the limiting measure and equivalently look at Green function estimates which are hard since we are in the spectrum. It is something which already in much simpler situations like almost Matthieu involves Diophantine considerations and math close to hard implicit function theorem (KAM) stuff. In random situations or almost periodic systems one has been able to tame the beast. The problem with the standard map is that there are almost periodic parts on positive Lebesgue measure and (unproven) random parts on positive Lebesgue measure. It is kind of circular. If we could prove randomness, then also positive potential, but positive potential also implies randomness.]
The intro and exit pictures of the movie from last Saturday, show pictures which were taken on Friday. I was visited by a Peregrine falcon at one point, who was interested in the avata. I think that falcon must live in Memorial hall as one has installed places to nest for them there. The little drone would be no match for that falcon who can fly with 320 km/h and which is also heavier than the avata. [Update of Monday: I had been flying again today was visited again by the peregrine. It was too fast to get into the movie. Peregrines are known to be the fastest animals in the world ! Two frames were in. Here is the picture . An other picture can be seen to the right, shot on Monday, where the falcon is just above, scaring the intruder or hunting a possible prey. I think one should see the pictures larger when clicking on them.














