Finite Schild’s ladder

We have to adapt the geodesic flow in two situations: for manifolds with boundary or for manifolds obtained as level sets in other manifolds where we want to define the geodesic flow directly in the open set and not first pass to the Barycentric refinement. In both cases, we sort of deal with an open manifold. If we take the boundary away from a manifold with boundary, we get an open set. The codimension k manifolds in a n manifolds also produced (n-k) manifolds which are a priori just open sets: take an aribrary function g from the vertex set to and look at all simplices x which satisfy g(x)=A. This is an open set because every simplex y containing x also has this property. The discrete Sard theorem (see “A Sard theorem for graph theory” in the case k=1 and “discrete algebraic sets in discrete manifolds” and the ultimate generalization “manifolds from Partitions” . The catchy version just used which is a special case when the partition is trivial is covered in the handout “Unit 18: discrete manifolds”[PDF] from a diffequantial geometry course of last fall. Discrete manifolds of course cover all differentiable manifolds as every differentiable manifold naturally has a PL structure. Also the embedding is not a restriction by Whitney’s embedding theorem and for Riemannian manifolds because of Nash’s embedding theorem. Embedding in an ambient space of course is still a bit ugly as it is not intrinsic but it is nice to know that it is not a loss of generality and it also allows to construct manifolds randomly. Here is where the discrete shines because for every q-manifold M, we get naturally probability spaces of q-k manifolds embedded in M if we want the manifolds to be written as “discrete algebraic sets” meaning being given from a random function g. The amazing thing in the discrete is that all functions work! This is different from the continuum, where already for polynomials we get algebraic sets which can have singularities. There are no singularities for discrete algebraic sets! (provided of course that we take the definition as just mentioned).

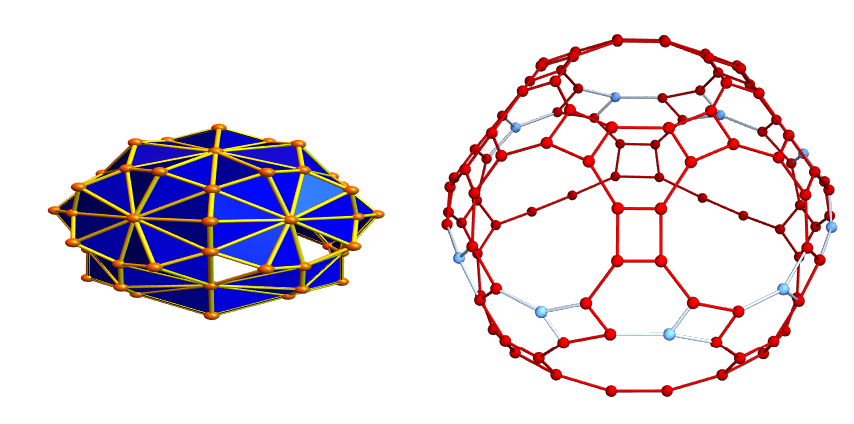
We had defined the geodesic map as a permutation T on the frame bundle P, where the later is just the set of all ordered facets (=maximal simplices) in the manifold. This is very nice and we want to extend this to manifolds with boundary and for level sets of manifolds embedded in an ambient manifold. I started to implement this for manifolds with boundary yesterday before biking in talking about this (see below) and experimented a bit this Sunday morning with embedded manifolds. It seems to work and I just want to share some pictures. There was a surprise, which after thinking about it is not such a surprise any more: the map on the frame bundle is no more a permutation in general, if boundaries are invoked or if we look at level sets. For level sets this is not a surprise given that we look at the frame bundles coming from frames in the ambient space. If we look at a 3-manifold embedded in a 4 manifold for example, then the geodesic flow on the ambient space is of course a nice permutation. But when restricting to the level set which is a lower dimensional manifold, then we should have an induced frame bundles. Not all ambient frame bundles are different on the manifold. This is also classically the case. The same idea I mentioned in the talk by the way also works for manifolds with boundary. Actually, we can think of an embedded manifold as a manifold with boundary. But this is dangerous thinking as seen in the very simple example given in the talk: the boundaries at different parts of the manifold can be the same. They touch even so the open sets do not. This forced us to look more fundamentally at the evolution on open sets and actually it is more natural than going to evolve on the boundary, even if we just look at the billiard in a manifold with boundary.

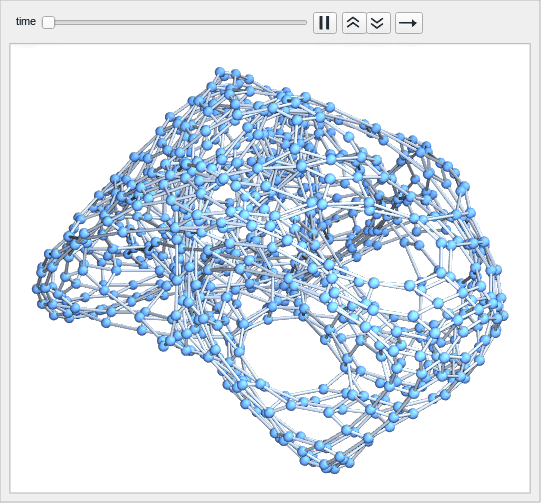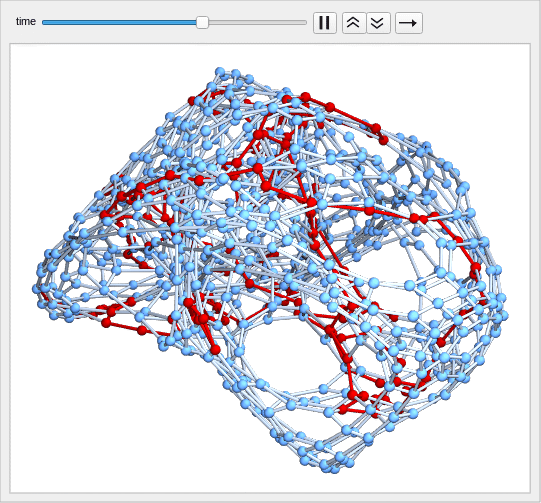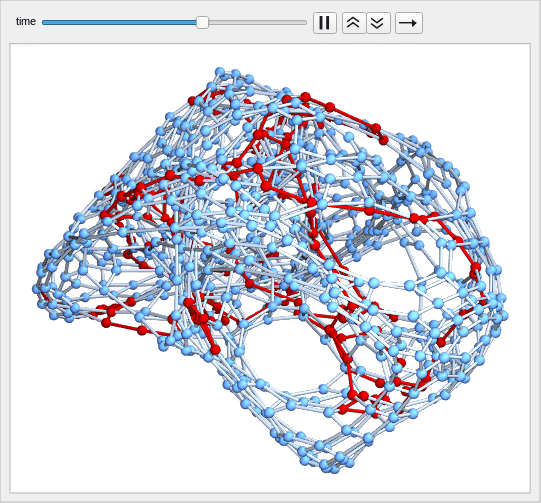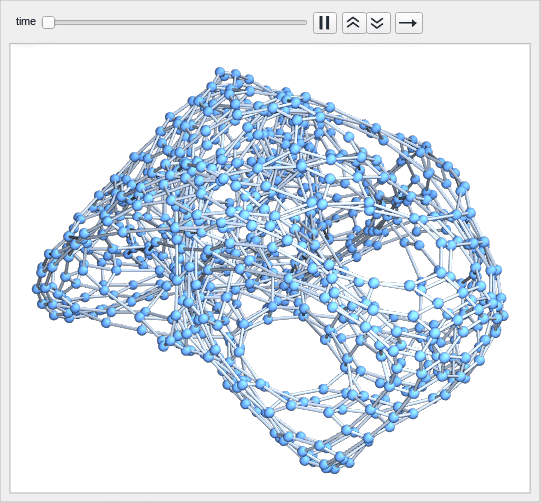
Let me say something about The Schild’s ladder idea. I had learned about it when teaching a course on geometric analysis which also included an introduction to differential geometry and general relativity. Here is a Gallery of illustrations for the book “Selected Topics in the theory of calculus of variations” to which I wrote the script. The book is here as a PDF and the illustration of the geodesic flow (written in Povray) is on page 64. I rewran some of the files for the differential geometry course taught last semester and here is a short featuring also some Povray animated pictures. The Schild’s ladder idea is due to Alfred Schild (1921-1977, he died early which is not a surprise that he was a heavy smoker. I don’t find the picture right now but showed a picture of Schild smoking last fall). The method is featured in the book “Gravity” of Miesner,Thorne and Wheeler from the early 1970ies (I always brag that Wheeler is my grand-grand dad). The book appeared just shortly after Schild suggested the idea of using the ambient space as a tool to compute the parallel transport and geodesics. The idea is very simple. Just think about the surface as attractive. You now move along in the ambient space but get dragged to the surface. This produces the geodesic flow. This happens for example on earth. Assume no friction and the earth to be perfectly smooth. Take a ball and roll it. It will try to move on a straight line in three dimensional space but gravity pulls it to the surface. The ball will move on a grand circle. It is actually much more interesting. Assume the surface of the earth is sprayed with a nice coating making it perfectly smooth but keeping hills and valleys of course. This is a two-dimensional Riemannian manifold. The geodesic flow is likely very complicated. It is a flow on the unit tangent bundle and so a flow on a 3-manifold. Most likely there is positive entropy for that flow but nobody knows of course. There are metrics on the 2-sphere for which the geodesic flow is ergodic. Victor Donnay has been a pioneer there (he was visiting the FIM when I had been a graduate student) and constructed various examples like here. Schild’s ladder became famous with the novel of Greg Egan. I actually tried to read it about 20 years ago but never succeeded finishing it. It is considered the “most difficult SciFi novel”. I mentioned the novel in this article from 2013 about even dimensional graphs. I had been fascinated at that time already from the fact that we can see the symmetric Morse index at a point in terms of the Euler characteristic of a co-dimension 2 manifold in the unit sphere S(x). At that time, I had not yet the discrete Sard theorem and had to dance around what it means to have a level set as the simplices on which on the unit sphere S(x) changes sign. The result discussed there is also true in the continuum when looking at very small spheres near a critical point and assuming f is Morse.

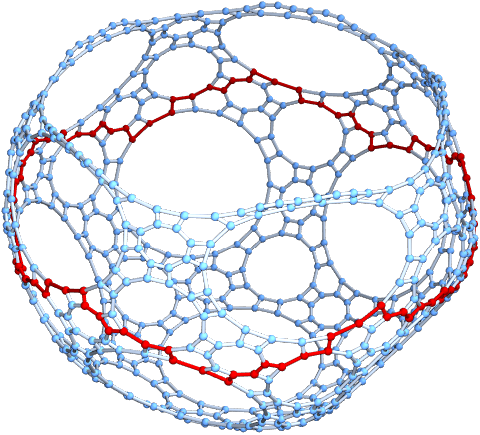
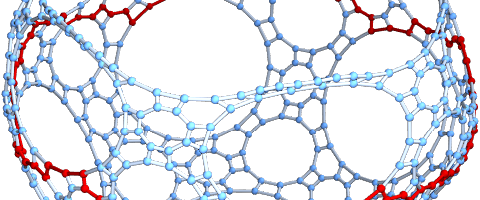
Now, in the discrete, I thought again about the Schild’s ladder idea. The reason is that the geodesic update rule can throw us out of the manifold (like when reaching the boundary) or when the next triangle is not part of the level set any more. In that case, we have to “curve” the geodesic” and turn the frame a bit to stay in the manifold. This is exactly what happens when we look at the geodesic flow on a manfold., we evolve on a straight line but then change course because we have to stay on the manifold. When looking for a scheme to solve this, I had pondered several ideas. One of them was to reflect at the boundary by evolving the geodesic flow on the boundary for one step. This actually works and had produced billiard flow dynamics for manifolds with boundary. But there was a problem when doing this for embedded manifolds. The reason is simple. There is no well defined boundary in general. We can for example have one dimensional curves (discrete Peano or Hilbert curves) which are one dimensional but fill out the entire manifold. These are Hamiltonian paths in the dual graph! They reach every facet in the manifold, but still are one dimensional. Such issues also appeared, when looking at the Jordan Brower theorem for graphs 10 years ago. We have to say clearly what we mean with a closed curve on a 2-sphere. You can in the finite easily draw a closed curve on the manifold which is Hamiltonian. Actually, all discrete manifolds are Hamiltonian, as I showed in 2018 with an inductive swiss cheese argument: as every unit sphere is Hamiltonian, we can cut out holes like in a swiss cheese ,then build Hamiltonian paths on the boundary of each hole, then connect them with bridges and make detours to reach the center of the holes. Here is a picture of a geodesics. To the left a complicated one reaching boundary of a half dome, the right shows a geodesic (again in the dual manifold) which does not hit the boundary.