Fisk Manifolds

The Regge approach to discrete relativity is also related to graph coloring problems of d-manifolds. While one can look at the length of the dual sphere of a codimension-2 simplex as a notion of curvature, the distinction of whether this circle has even or odd length is relevant when wanting to color the d-manifold. I started to work on topological graph colorings in 2014, now 10 years ago. It was sparked by a a HCRP project of Summer 2014 with Jenny Nitishinskaya, we explored coloring of manifolds. At that time, I had been looking at the discrete Sard theorem and naively thought that this would help to color manifolds and even aim for showing that 2-manifolds are 4-colorable. Jenny found a projective plane with chromatic number 5. I learned about Fisk theory in December 2014. There is a conjecture of Albertson Stromquist asking whether any 2-manifold can be colored with 5 colors. This is open so far. There are tori or projective planes which need 5 colors but no example of a 2 manifold with chromatic number 6 is known. [Even so it is explained at various places and in detail in this paper, it might still also important to stress that manifold coloring is in dimension 2 and higher very different from the coloring appearing in topological graph theory where one can embed a into a 2 torus. The graph is not a 2-manifold but a 6-dimensional simplex. The coloring of d-manifolds we were interested since 2014 does not involve the continuum at all. It deals with graphs which are axiomatically in a recursive way defined to be d-manifolds. It is just combinatorics. See some slides from 2014 [PDF] and on youtube from December 2014, pretty much 10 years ago. ]

Define the Fisk manifold as the collection of codimension 2 simplices x in a d-manifold for which the dual sphere has odd length. This dual sphere of x in a d-manifold is always a circle if x has dimension d-2. In dimension d=2, the Fisk manifold is a 0-manifold and given by the set of vertices for which the vertex degree is odd. For dimension d=3, it is the set of edges for which the number of tetrahedra containing this edge is odd. In dimension d=4 (the Regge case interesting in discrete relativity frame works), it is the set of 4-dimensional chambers ( graphs) which are attached to this triangle (sometimes called “bone” in discrete GR). The dual sphere of x is the intersection of the unit spheres of all its vertices. It is again a circle because it is the unit sphere in a unit sphere in a unit sphere.

The Fisk manifold is a priori just a collection of (d-2) dimensional simplices. It an be partitioned (not uniquely) into parts which each generate a (d-2) manifold. If the underlying manifold was a d-manifold with boundary, the Fisk manifold is then a union of parts which generated (d-2) manifolds with boundary. In the case d=3, if we look at the Fisk manifold of a discrete 3-ball, then the Fisk manifold can be decomposed, so that each part is either a knot or a tangle, a path starting and ending at the boundary (possibly knotted). The discrete 3-ball looks special but it is of greatest interest as the 4-color theorem follows from the statement that one can reduce the size of the Fisk manifold by edge refinements.

Heawood type statement: a d-sphere is (d+1) colorable if and only if its Fisk manifold is empty. For 2-spheres, this means that the graph is Eulerian. (See: Graphs with Eulerian Unit spheres from 2015.) See also “Coloring Discrete Manifolds”, where the upper bound 2d+2 for chromatic number appears for d-manifolds which is based on that the point arboricity of a triangle free graph (the dual graph) is less than 3: make the Heawood coloring on one of the trees and a second batch of Headwood colorings on the other. Between 2014 and 2021 there had been a shift. I originally thought that a d-sphere must have chromatic number d+1 or d+2 generalizing the 4-color theorem which is equivalent to a 2-sphere having chromatic number 3 or 4. But spheres form a monoid under the join operation and the chromatic number of the join obviously is just the sum of the chromatic numbers of the summands. If we take the join of a circle of length 5 with itself, then the chromatic number of the resulting 3 sphere is already 6. We have no example yet of a 3-sphere with chromatic number 7 or 8 and this might not exist.

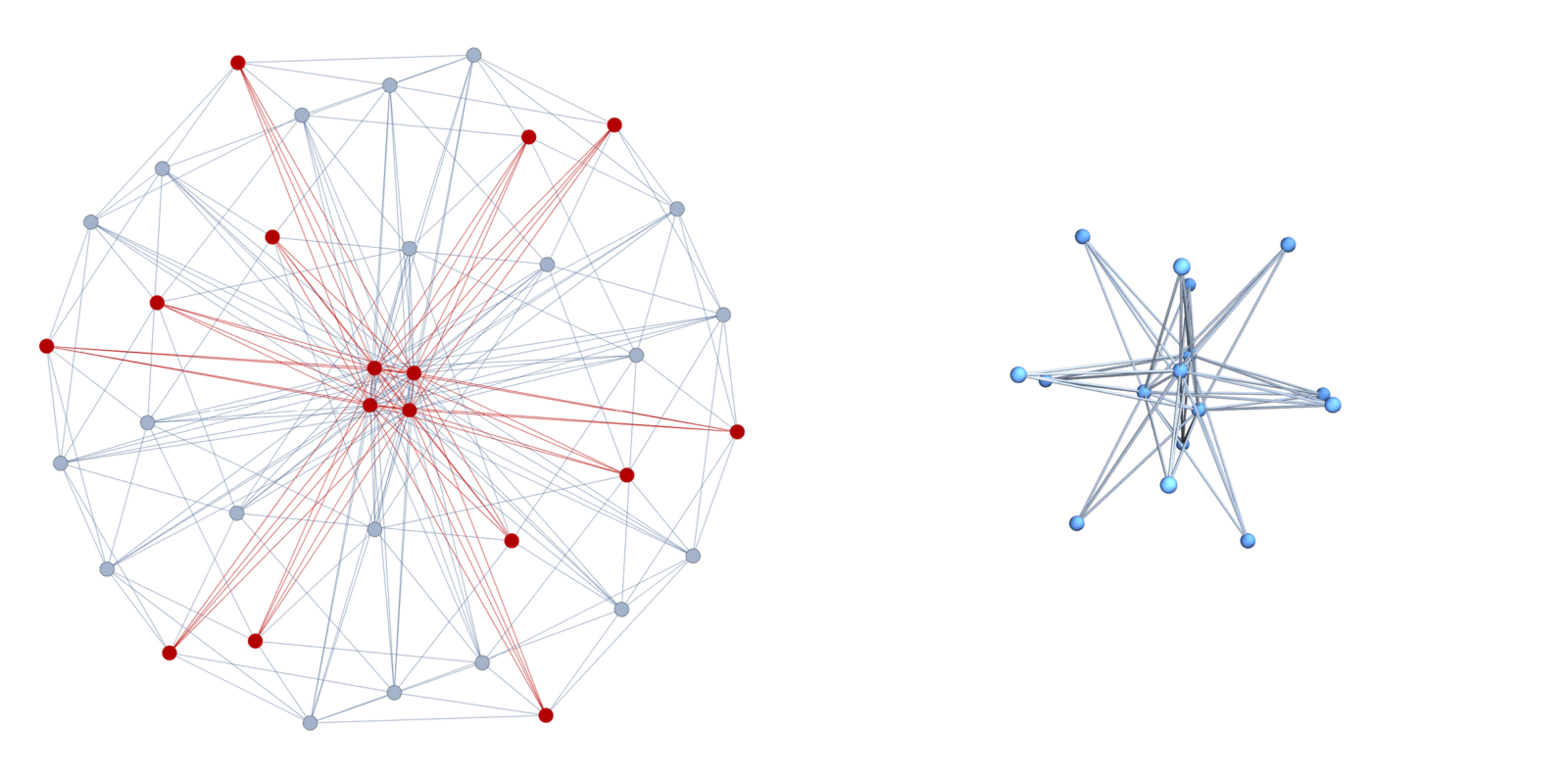
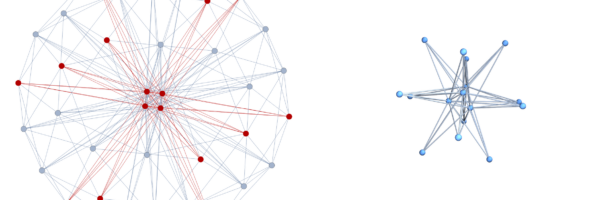
My interest in the coloring problem again was more recently again raised because of the observation that soft Barycentric refinement does not kill the Fisk manifold but that it just produces a Barycentric refinement of it. This can be illustrated already very well in dimension 2, where the Fisk manifold consists of the set of vertices of odd degree and where soft Barycentric refinements do not change the Fisk manifold. The soft Barycentric refinement does not change these vertex degrees but adds more vertices with 6 neighbors. The picture to the right shows a 4-sphere obtained by taking the join of an icosahedron with a circular graph. The Fisk manifold is a union of 12 octahedra. They are not disjoint.