Fundamental Problems in Discrete Differential Geometry

Here are two fundamental problems for discrete q-manifolds (a notion which can be defined for the trinity of geometric structures, that is for finite simple graphs as well as for simplicial complexes or delta sets).

Define a simple sectional curvature so that classical theorems hold.
Define a simple geodesic flows so that classical theorems hold.

As for 1, one could ask that every embedded wheel graph has positive curvature. This turns out to be too strong because every positive curvature manifold of this type is a sphere. As for 2, the shortest connections between vertices are already non-unique in distance 2. The radius of injectivity is 1, independent of the manifold. Also that is unacceptable if we insist to have classical theorems to hold. Questions 1 and 2 are not yet precise if we have not stated what “classical theorems” are. For 1, we definitely want that a positive curvature notion selects the known positive curvature (q=2n)-manifolds $S^{2n},RP^{2n},CP^{2n},HP^{2n},O^2,W_6,E_6,W_{12},W_{24}$ (which are conjectured to be the full list and which have affinities with bosons) and that the sphere theorem holds: sufficiently pinched positive curvature manifolds are spheres. As for 2, we want a global dynamical system on the manifold (something defining exponential map) and be able to connect any two points by a geodesic and also want a radius of injectivity that makes more sense. There is no way, we can define a local law like the law $\ddot{x}^k=-\Gamma_{ij}^k \dot{x}^i \dot{x}^j$ in the continuum, simply because any law that only involves a given sized neighborhood of a point only allows for finitely many different geodesics to get out. This is not enough to connect any two points. Take already a hexagonal flat 2-dimensional plane. To reach all points in distance r away, we need 6r different geodesics to start at the same point. In a combinatorial setting (which we always assume of course), there is only a finite amount of information in a given finite neighborhood.

Here are some ideas:

In order to define the flow for larger distances, look at more and more refined manifolds. Define therefore the geodesic flow not for a single manifold but for a sequence of more and more refined manifolds. I’m currently not interested in that because this is a numerical scheme. It is similar as when using rational numbers to approximate real numbers. We can of course do numerically everything with ratios of integers but this is just a basic numerical principle and nothing deep and does not provide us any understanding without studying how good the approximation is etc.
Nash embed the manifold in a given Euclidean manifold and use the underlying classical theory. This is terrible for the simple reason as it is just the classical theory in disguise. This is nothing new. This happens if we make a numerical computation of geodesic flows on a computer. Every computer invokes only finitely many bits but manages to numerically work. I’m not interested in that in the above context simply because it has been done for centuries. The embedding idea is still useful as it produces a bridge between the finite and the continuum with the help of integral geometry. We can use the embedding to get probability spaces on functions on the discrete manifold which then via expectation define curvature. We should point out that in general, “engineering approaches” are just ugly. They are effective, yes, but ugly. Usually, beauty and effectiveness are complementary. It is what poetry is to an instruction manual.
Work in a Vietoris-Rips setup where manifolds are generalized. I myself followed this in 2021. Define axiomatically a more general class of graphs (I had called q-foam or homotopy manifold) which have the property that every unit sphere is either a (q-1) foam sphere or then contractible. A sufficiently dense random point cloud on a given classical manifold is q-foam. If we take away points for which the unit sphere is contractible, we end up with a manifold. q-form manifolds are of the same homotopy type than q-manifolds and so have the same algebraic topology. They are topologically however different already because the dimension is very large in general. The frame work is still very natural and graph theoretical geodesic paths pretty well approximate classical paths. For me it is still just a numerical scheme, a Monte-Carlo scheme in geometry. I talked about this set-up here in May 2021, during a dystopian time, where we already could enter our offices but only after having filed for a request to enter during a specific hour, after testing and in each floor of the building only a few time spots were opened.
Work in a quantum setup, where we forget about classical paths and look at solutions to the wave equation $u_{tt} = - L u$ for a Laplacian $L=D^2=(d+d^*)^2$ which has basic solutions $\cos(Dt)$ and $\sin(Dt)$ or $e^{\pm i t D}$ in the complex which are solutions to the Schr\”odinger equation $u_t = \pm i D u$ for the Dirac matrix. Related is the operator $L_X = d i_X + i_X d$ (which by the Cartan magic formula) gives us some sort of direction given by the vector field. In any case, when wanting to define a light ray (laser) we want solutions to the wave equation that are localized. After centuries of debate about whether light are waves (Huygens) or particles (Newton), the 20th century brought more insight, in particular with Einstein’s photoelectric effect paper, experiments of Millikan or Compton leading Gilbert Lewis to coin the word “photon” in 1926. Since we are able to produce sharp beams of laser light (where nobody really explains nicely why these beams are not decaying, try to do that in a water wave), this should also be possible in the discrete so that we could model geodesic flows without the constraint of classical paths. This is possible in the discrete. We can look for example at initial conditions u(0) of the wave located on a vertex v and ask to be supported at a later time u(T) at a different vertex w. If T is large enough, we can find an initial velocity u'(0) with such a solution. This is a “photon” traveling from v to w. So, for me as a mathematician who needs precise definitions of things, one could define a “photon” as a solution of a wave equation that is localized at some time at one vertex v and at an other time at an other vertex w. If these solutions span the entire Hilbert space, we have a more “sensical” explanation how to see a wave being made of photons. The eigenfunction picture given in quantum field theory does not provide a good intuition why “photons are localized”. In the quantum mechanics course I myself have taken as an undergraduate, Klaus Hepp told us to find our own explanation about the “particle-wave duality conundrum”.
Work in the dual manifold. That is actually something I consider very promising at the moment, as the dual manifold (the vertices are the facets and two are connected if they intersect in a (q-1)-simplex) have a nicer geodesic flow ,simply because the dual graph is triangle free and does not have such a small radius of injectivity. The fundamental cycles in the dual manifold are defined by (q-2)-simplices (= bones) $x=(x_0, \dots, x_{q-2})$ . The dual $\hat{x}$ of a bone $x$ is defined as the intersection of all unit spheres $\bigcap_{k=0}^{q-1} S(x_k)$ . In a q-manifold it is a circular graph with 4 or more elements. These are the two dimensional cells in the dual manifold. In general, the k-dimensional cells in the dual manifold $\hat{G}$ are defined by the $(q-k)$ -dimensional simplices in the manifold $G$ . This is a nice approach to duality which historically (similarly as the notion of “polyhedron” or “manifold”) has had a hard time to be born. Even Poincar\’e got duality wrong at first and needed to fix this after critique of Heegard (a friendly euphemism as “critique” actually means “errors”). Also the notion of “manifold” was fixed only decades after Poincare particularly through work of Hermann Weyl (1912) Hassler Whitney (1930) or Oswald Veblen (1922) . As for duality, a fundamental difficulty is that the dual of simplicial complexes (as defined by Dehn and Heegard from 1907 [purely combinatorics without Euclidean realization]) is not a simplicial complex in general. Already the dual of the octahedon, which is the “cube”) needs classically in the discrete the concept of a discrete CW complex, as the cube is triangle free. We can spot the 2-dimensional cells without having to embed them into Euclidean space (and performing a fundamental betrayal of finite combinatorics which should remain discrete and not use the infinity axiom). The faces of a dual 2-manifold are the cycles in the dual graph which are the intersections of all unit spheres of the (q-2)=0 cells in the graph itself. The dual sphere approach works in any dimension and is elegant. Similarly as with other topics like “product manifold” or “submanifold” as level set or “quotient manifold” or “open sets in a manifold” we need also for “duality” to work in the larger frame work of delta sets as these basic operations leave the category of simplicial complexes. Duality again confirms that delta sets are natural, also for a practical working mathematician and not only because of poetry lovers admiring topoi.

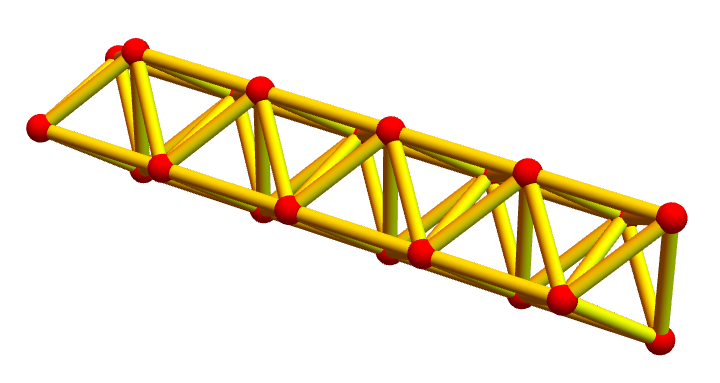
geodesics in 3 dimensions. The boundary surface has zero curvature

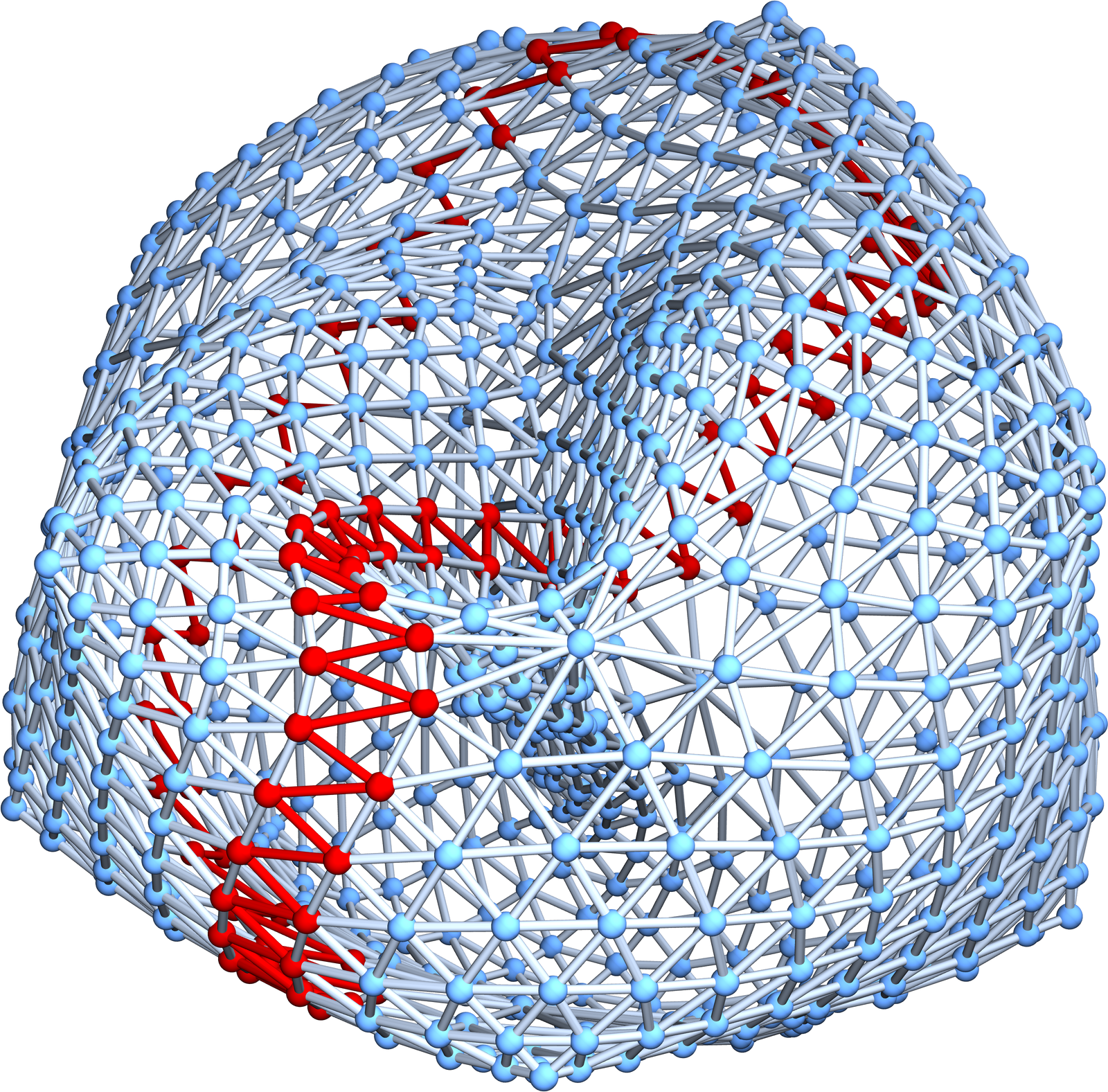
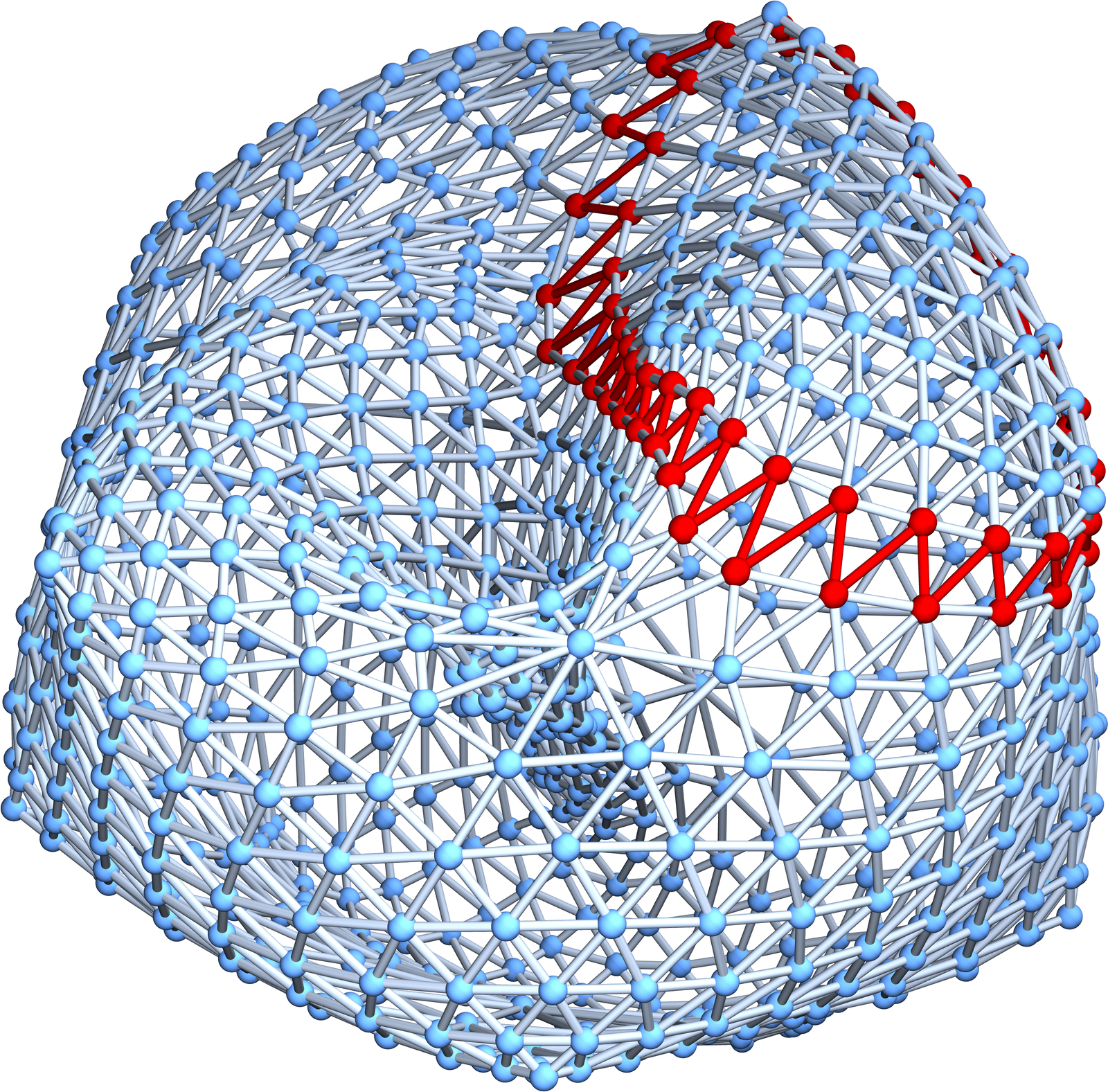
Over the holidays, I had been thinking more about the approach in 5. Working in the dual manifold seems having the property that we can define a global geodesic flow. Lets look at a 2-dimensional manifold for example. We can look at a “strip of facets = strip of triangles” as a geodesic path if the boundary curvature of that strip is zero. This means that the vertex degree of each boundary point is 4. This is a very nice analogy to the continuum as we can see the boundary curvature as some sort of “geodesic curvature” and so have that “a geodesic is characterized by the property that the geodesic curvature is zero”. This can work in general. It is natural also from the topological point of view. I had been interested in this 2 winters ago as level sets in manifolds are a priori open sets. This by the way had been the theme which occupied me last winter (see here and here). By the way, the topic of discrete manifolds turned out to be teachable which is always a good sign that something really works. Teaching is a good way to engage into a topic and while teaching classical differential geometry, I also thought about how to define “geodesic curvature” in the discrete. The most natural way as for now appears to me to define this through the curvature of the boundary of the curve (which is a hypersurface as it bounds a set of maximal simplices). One can then also try to look at the boundary curvature of an embedded (q-1)-manifold and look at such sheets which have zero boundary curvature as “geodesic sheets”. The intrinsic curvature (which of course is different than the embedded curvature) then is what should be “sectional curvature”.

Update of January 6 2025: Here are two geodesics in a soft Barycentric refined projective plane. We should actually have drawn the triangles. The point is that we look at geodesics in the dual graph, which is much better behaved than the graph (the radius of injectivity is always 1in a manifold). The highlighed points should actually be replaced by triangles. The connections are pairs of triangles which intersect in an edge. This defines an open set U in the Alexandrov topology of the graph (projective plane) and the boundary, the complement of the complement and the open set U (This is classical finite point set topology, but not Alexandroff topological spaces of finite abstract simplicial complexes (generated by stars in the complex) are never Hausdorff in positive dimension), consists of two closed circles which actually have zero geodesic curvature in the surface! This works also in higher dimensions. There is a unique dynamical system with discrete time and does not assume the 2-manifold to be Eulerian. The system also can be Coxeterized, meaning that the dynamics can be generated by two involutions. (That is extremely important to me, as the integers are not a “natural” frame work. Kronecker was wrong. The correct statement is God created the dihedral group and everything else is human made. The integers do not form a natural group because it is not determined by a metric space. The dihedral group on the other hand is up to isomorphism the unique group isometry structure on some metric space. I wrote about this here. [I still doubt that kids in 200 years will learn the dihedral group before the integers but it is not impossible because of the difficulty to motivate negative numbers already (this Grothendieck completion is taught by indoctrination and “I told you so!” and actually incorporates concepts like equivalence classes). For the dihedral approach, 1=ab, 2=abab, c=ababab etc and -1=ba does not need any completion. The negative numbers are already there. The addition ab+ba=abba=aa=0 is a “candy crush” concept. While it is probably not for everybody, I can imagine that the dihedral group can convince a small kid already that mathematics is not just doing what has been done for thousands of years but that it is vibrant field that constantly changes and that there are many ways to do things, some natural, some less natural, and that we have not even started to develop a tiny part of the entire field. ])

Author: oliverknill