Groetzsch’s Theorem

Herbert Groetzsch and Jan Mycielski worked in the 50ies on the chromatology of triangle free graphs. Groetzsch’s 3 color theorem assures that planar triangle free graphs have chromatic number 3 or less. Mycielski defined an operation on graphs which preserves triangle free graphs and increases the chromatic number exactly by 1. By nature, these graphs are very small in the sense that there is a point whose ball of radius 2 is the entire graph. This is not possible for dual graphs of manifolds except for the 1-manifolds and . 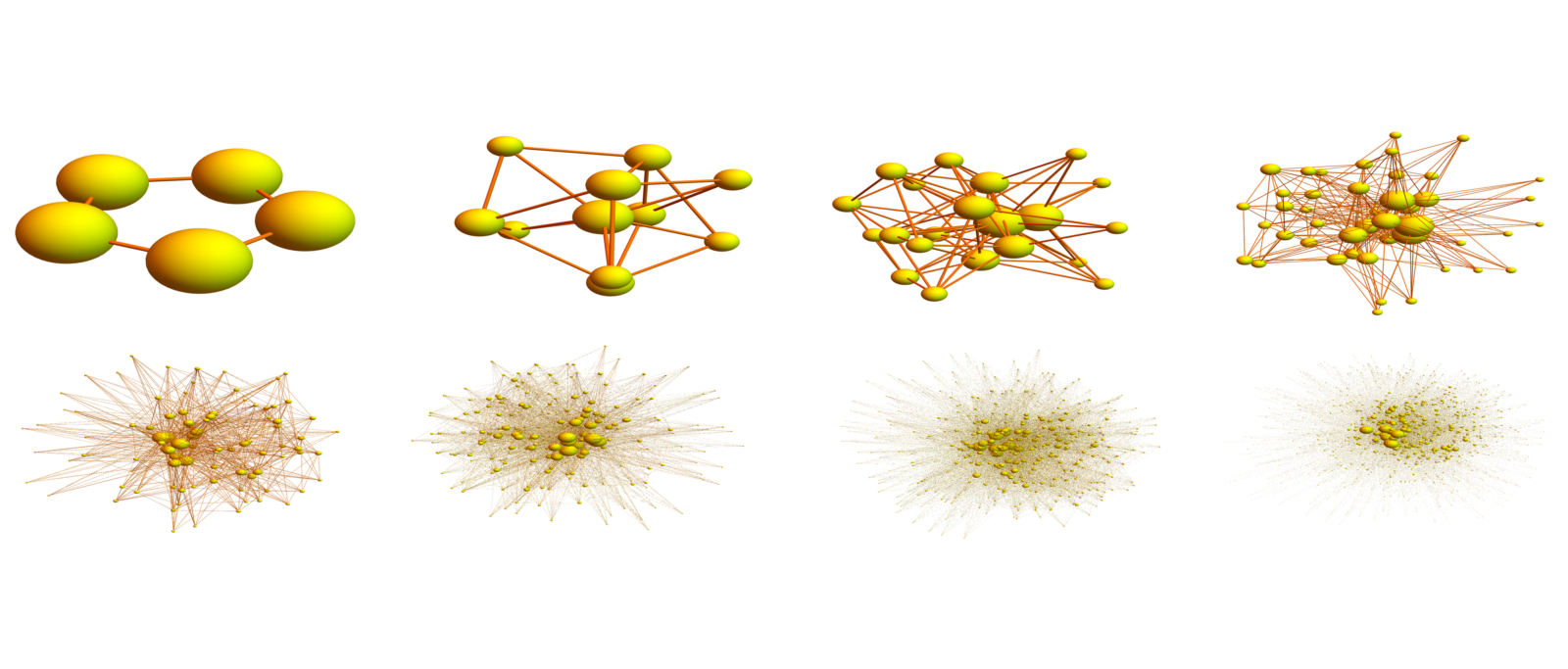Already the cube graph, the dual graph of the smallest 2-manifold does not have this property. (There is more at the end of this post about all the confusions and refutations (and maybe psychology) of manifolds and coloring research, especially in higher dimensions). What happens with dual graphs of discrete manifolds is that there is enough structure to prevent collision situations that occur in Mycielksi examples. I talk about this in the video. Below are a picture showing the first Mycielski graphs. I plotted them with the size of the nodes indicating the vertex degree (this is an other difference to dual graphs of q-manifolds, where the vertex degree is constant q+1). What happens for dual graphs of manifolds is that their chromatic number is always 2 or 3. And 2 happens for if and only if the Fisk manifold (formed by the q-2 simplices for which their dual cycle is odd) is empty. One can this theorem also inductively with respect to the dimension q. For q=1, it is clear as then the dual graph of is which can be colored by 2 or 3 colors depending on whether n is even or odd. And for q=2, it is essentially the Groetzsch theorm. I try to write down a short proof of this 3-color theorem for arbitrary q.

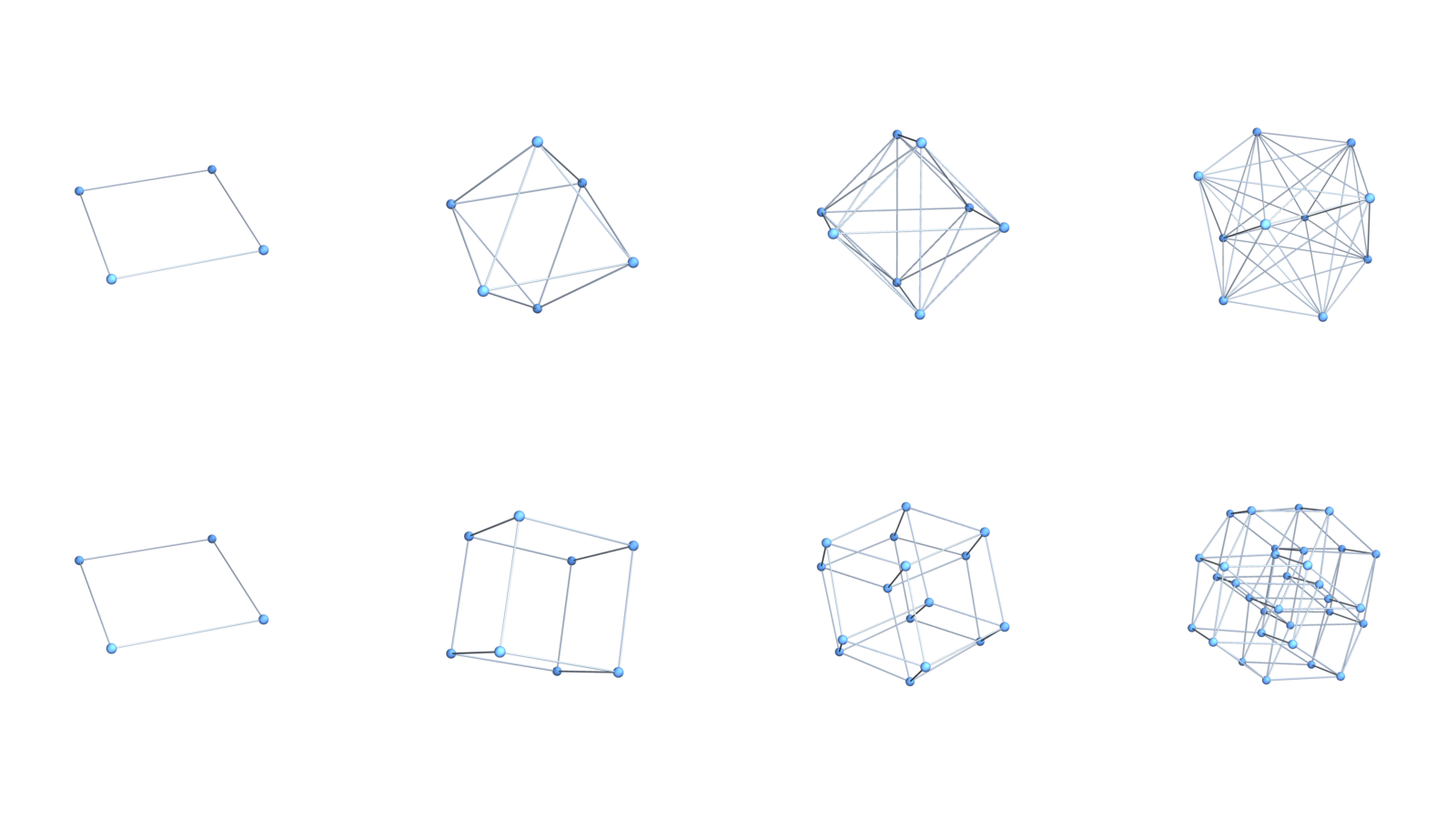
Here are the smallest q-manifolds for q=1,2,3,4 (which are cross polytopes and below their dual graphs (which are hypercubes). All these dual spheres can be colored by 2 colors as their Fisk manifolds are empty. The dual cycles of any bone ((q-2) simplex) is a circular graph of length 4.

Mathematics is a huge world. Almost nothing is explored yet. So, in most places one ca experience to be an explorer. The trouble is not so much to find a nice place, there are plenty. The difficulty is to choose a quiet place which still is nice. For a younger mathematician, it is important to work on a subject that is popular and gains lots of interest. The reason of course is that one needs to worry about getting a job. Being able to do research has become more and more a luxury, something less and less can actually do as the selection process is more and more a lottery (there are so many factors which are out of control). For an older mathematician like me it is more desirable to have a topic in which one can explore without too much competition. In the tourist allegory, I prefer visiting a tropical island without mass tourism. The advantages are obvious. If you are in a remote place, there are lots of discoveries possible, there might even be unknown treasures hidden. They are there simply because nobody has been there to look at them. The treasures are also beautiful if nobody else looks at them. I myself would do math, if I was the only person on this planet. As a teenager of course, this is not an option, you want to be where everybody is and where the party is loud.

The topic of coloring discrete manifolds is maybe one of these treasure island places, which nobody visits. That is the best thing which can happen to a mathematician. If the place would be crowded, all the nice things would be gone already. You might ask why I then talk about this in the Youtube video below. The reason is simple: nobody watches it anyway (my family call my youtube efforts as “talk to yourself sessions”.) So, why making these videos? For me, it is because it helps to arrange thoughts and also to get organize and remember. It is harder and harder these days to get off the electronic chains which bind and paralise us (computers, smartphones especially). Creative thinking can better be done away from the computer, by thinking and talking about it without just looking things up or rehearse. Youtube is a nice “pensieve” (in the sense of the Harry Potter books) to store thoughts in a more immersed way than in writing. I myself change mathematical topics rather quickly and so also forget relatively fast what I have done previously. Now, I can go back and look at how I thought about a particular subject. If I look at old research diaries from my graduate time (I still have drawers full of them), then I hardly understand any more in which mindset I was when writing it. It would be easier to see into the old thoughts when having recorded unscripted talks.

There are lots of reasons, why higher dimensional manifold coloring is not a popular research topic, (a fortunate fact for me). One of them is that most graph theorists are still stuck in the 20’th century perception and see graphs as “one dimensional objects”. Maybe because I was not grown up as a combinatorics person, I can not understand this point of view. It is like seeing the 2-dimensional plane as a 0-dimensional object because it is made of points. It is the structure on which one builds things is not that relevant. What is important is what additional structure one naturally has with it. On a two dimensional plane we have a natural metric structure. Similarly, on n a graph, one has a natural simplicial complex structure which everybody immediately sees, when looking computer graphics of triangulated surfaces or solid. If we look at a crystal graph, we immediately see a higher dimensional structure. The triangles form natural 2 dimensional parts and tetrahedra form natural 3 dimensional parts. Traditionally (last half of the 20th century) one adds higher dimensional structure by embedding them into continuum manifolds. This is what “topological graph theory” is about. When embedded in a 2 dimensional manifold, there are by the Jordan curve theorem then naturally “faces” popping up. When looking at coloring problems in higher dimensions, this point of view becomes problematic. How many colors are needed to color a triangulation of a 10 dimensional manifold? It very much depends what one understands with triangulation. Already a 2-torus can be triangulated with a graph needing 7 colors. In higher dimensions, the mess gets even bigger. The solution to the problem is to leave the beaches of Malibu, Copacabana or Santa Monica where everybody goes and go to places that are less crowded. That’s where one can still discover things easily with have not been seen before.

The problem of manifolds coloring is a paradise, if one cuts all the nonsense and confusion which can come from the continuum and looks at manifolds independent from the infinity axiom (meaning that never, ever any embedding or relation to a continuum like the Euclidean space is assumed). Define what a q-sphere and q-manifold is recursively by demanding that in a q-manifold, the unit sphere of any vertex is a (q-1) sphere and that a q-sphere is a q-manifold which has the property that if one vertex is removed it becomes contractible. This is not only elegant, it is also beautiful, practical and the recursive nature allows to prove things easily. A 2-manifold is a finite simple graph for which every unit sphere is a cycle graph with 4 or more elements. Already now, we get into interesting unsolved problems. I have an upper bound for the chromatic number 2q+q for a q-manifold which gives an upper bound of 6 for 2-manifold. It is relatively easy to construct manifolds (different from the 2-sphere of course) which need 5 colors. The 4 color theorem is equivalent to the statement that a 2-sphere can be colored with 3 or 4 colors. [The reason, why I talked about so many times since 2014 also because my original intuition before 2014 was that “coloring manifolds is easy” was completely wrong after realizing in 2014 that a result essentially proven by Whitney shows that if we can color 2-sphere, we can color any planar graph, Walter Stromquist once called such arguments as something everybody starting to work on the subject at some point must have discovered independently: it is hardest to color maximally planar graphs and a decomposition argument shows that we only have to consider 4 connected planar graphs and it is now a matter of fact that 4-connected maximally planar graphs are either (the tetrahedron) or a 2-sphere. There is nothing more “character forming” in mathematics than having its own intuition seen proven completely wrong. My original feel that it is “easy” to color 2 manifolds has cut deep, but it was also rewarding. There is solace in the fact that historically, some of the brightest mathematicians got intuition about coloring problems wrong.] The main argument one can give to convince anybody that the subject of manifold coloring is interesting is to point out that an old conjecture of Albertson and Stromquist asking whether every 2-manifold can be colored with 5 colors. [Again, one should stress that there is almost no connection with the story of the Heawood which is a completely different manifold coloring story, that only by accident overlaps in the case of 2-spheres.] The problem is wide open. I myself can only show that 6 is the upper bound. No manifold is known that has chromatic number 6. I myself believe that 5 is the upper bound and that the conjecture of Albertson and Stromquist is true and that its difficulty could be of similar severity than the 4 coloring theorem (“2-spheres have chromatic number 3 or 4” implying the almost equivalent statement that “planar graphs have maximal chromatic number 4”). But the subject of graph coloring is always good for surprises and I would not be surprised to get surprised. And that is one of the charms of this “treasure island”. There is nothing nicer than being surprised.