What is the reason for the structure of the Standard Model? For a mathematician, it better has to be something inevitable. The model is the periodic system of elements is all based on the geometry of the space G one considers. If G has an exterior derivative, one has a Laplacian , an inverse integral operator defining a potential
and so a hydrogen operator
. The spectral properties of H (the eigenvalues
then essentially define the periodic system of elements. This can be done in any space, also on a finite space. So, since Chemistry is determined in this rather simple way from a simple geometric structure (Euclidean 3-dimensional space), it is natural to ask, whether this is also possible for Physics. Can one explain the structure of the Standard model from basic mathematical principles, similarly as the Mendeleev structure of constituents is determined by the Laplacian of 3-space? Since the structure needs to be inevitable, one better looks for algebraic structures which are rare or better, structures that are unique. There are such structures. The Theorems of Frobenius or Hurwitz allow to characterize the complex numbers as the unique associative, Abelian real division algebra and the quaternions as the unique associative, non-abelian real division algebra. The consideration comes also from the fact that electromagnetism is based on the gauge group U(1) which is the unit sphere in the complex numbers and the gauge group SU(2) of the weak force is the unit sphere in the quaternions. These spaces are the only Euclidean spheres of positive dimension which are also Lie groups. (There is also
as the unit sphere of $\mathbb{R}$). The strong gauge group SU(3) can be seen as an additional symmetry on the quaternions generated by the action of SU(3) on the space part generated by i,j,k. If one looks at things as such, it explains why one does not see something like SU(5), but this explanation is just a gut feeling. The attempts to get to the structure of elementary particles through division algebras is not new. Atiyah once suggested that the octonions might be related to gravity. Here are some links: https://www.quantumcalculus.org/quaternions-and-particles/ (a blog entry from 2016). And here is the “particles and primes” paper from August 2016. (I never attempted to submit that article. It would be much safer to play the lottery. The “positive curvature and bosons” paper (which is more heavy as it deals with the unresolved structure of the positive curvature manifolds), I had once tried to submit it in a physics journal, but immediately got rejected. I still think that paper too is very interesting. In both cases, there are curious analogies which relate mathematical structures with unsolved problems in mathematics. In the quaternion case, one has the structure of the these primes, in the positive curvature case, a nagging open problem in differential geometry. )
[A side remark. When googling “particles and primes” now, I found this book of Martin H. Krieger with the title “Primes and Particles”. The mathematician Martin H. Krieger just died on July 17th 2024. I looked at the book and there is nothing in common with the topic discussed here. It talks more about mathematical physics, like the Ising model, the stability of matter, the music of the primes, Thomas Fermi, zeta functions. The book appeared on February 23rd of this year 2024, just 5 months before Krieger’s death. It includes also philosophical parts like discussion about what “mathematical physics” is about or about “Creation: when something appears out of nothing”. One of the lessons seen in statistical physics is that order can come out of disorder .It is in general an interesting issue indeed: why there is at all something. The simplest “solution” to build a world would be to have nothing. It is the most beautiful solution, the most elegant solution, it is a minimum of complexity of problems. The theory “nothing” is beautiful because there is no explanation needed. Everything is clear. It is optimal. There are no ambiguities. But it is also just for “nihilists”. Apropos Nihilism: the topic comes up in the iconic “Big Lebowski” movie. Th relevant clips are here or here (youtube links). Unrelated to that there is even an antropic explanation why there is “no nothing”: In a world “nothing” there are no observers who can observe it. This is a joke of course but it brings also a less funny component to the discussion. One has used of anthropic principles like “landscape models” to attempt to doing serious physics. Sometimes one can be happy to be a mathematician and not a physicist. ]
[An other side remark: My 2016 write-up on particles and primes has had a hick-up when putting it on the ArXiv. The ArXiv is not peer reviewed but maintained, (bot ?) moderators who just filter out the most insane absurdities. The “Particles and primes” document had been flagged at first because of “self plagiarism” concerns, my experiments in number theory paper contained something about it. A recent “adventure with ArXiv” happened when submitting this article on colorful partitions. For two weeks, the submission had been put on hold, without any explanation. What must have happened is that some “AI” (I can not believe there exist “actual people as moderators” that are so superficial) triggered a flag. It would be nice to know what it was: it could have been the topic of Cuisenaire sticks, which is a manipulative from elementary school and definitely not a “traditional” way to reason in number theory. It could also be because of comments on education. In the context of Cuisenaire, I mentioned that my first grade teacher Herr Ilg still could control his teaching and take initiative like giving us Cuisenaire sticks to learn about numbers and that my teachers (from Kindergarden to high school) enjoyed quite autonomy and freedom. Today, the cancer of control has even started to take over higher education: intro calculus classes are more and more scripted with little autonomy for teachers. It is a vicious circle because creative folks will less likely go into the profession of teaching, forcing the administrators to control even more what is done in the classroom. Maybe it needs a wake-up call. The indisputable fact is that the K-12 education system in the US does not do well: “Compared to the 80 other education systems in PISA 2022, the U.S. average mathematics literacy score was lower than the average in 25 education systems” (Source). I myself would have no idea how to fix this. The way how it at the moment fixes itself is unfair: more and more wealthy families just send their kids to private schools (which do allow teachers to be more creative). Maybe, if public schools would start paying more for teaching, some of these creative teachers would consider transitioning to the public school. An other problem is that education has become more political. Similarly as with journalism, there are some who think that education should be platforms for political or social activism. The public trust in media or education has eroded substantially (I myself do not trust most of the media any more as they have become advertisement campaigns for various political issues, on all sides). I would not know how to fix things myself, even if I was in charge. What can help is to point out models which worked: when I went to school, the system has been pretty healthy. All my teachers starting from Kindergarden to high school were excellent, creative and used diverse teaching approaches which fitted their personality: some would like to tell stories in their classroom, others liked to have heated discussions, again others liked to give us ample of time to work on routine problems, again others liked to do unusual things. One of the elementary school teachers (Frau Rohner) taught us Polish dances during gym time (we learned it perfectly) or go to 12 km hikes in the woods. One of the middle school teachers (Eduard Schmid) would give us professional orienteering maps and compasses and lets us run competitive tours alone in the Cholfirst forest near Uhwiesen, the used to be stamps located at markers on trees throughout the forest and we had to race to get them. In chemistry, it had been possible for the teacher (Herr Borer) just to give us access to the entire chemistry lab with a task of figuring out the nature of some powder. Would this be possible today? No, what if a 12-year old would get lost in the forest or worse, get abducted, or what if one of the experiments with the powder would lead to an injury? Risk avoidance has become priority number one. I wrote once about the issue of “risk” in a yearbook letter of 2021 during the pandemic. Risk is a difficult issue. The dilemma is that local risk minimization is a Nash equilibrium but that the overall “benefit functional” is very low in that equilibrium. The safest way to survive is to move to a cellar, see no sunlight (skin cancer reduction), have no exposure to germs, not talk to people etc. The global “benefit functional” however is very low as basic psychological parameters are not considered (light and outdoor time benefits the mood for example and social interactions help too). Similarily, it is safest to give every teacher a “script” how to work through a specific lesson ,to make sure that every students get the same experience. One is surprised then however why the global benefit functional scores low. It is the curse of the Nash equilibrium! Getting out of a Nash equilibrium is very hard as it locally, it will produce less optimal results. As a mathematician, one of the things to try is to really assess well what the value functional actually is. What game theory teaches us that more sophisticated functionals which also take into account quantities that usually are not taken into account. This is a dangerous issue however because who knows which functionals are important and which are not? Is the goal to score high in PISA exams a good parameter? If not, what would replace it? Things can become political. (We even vote about this on Tuesday as some want to get rid of MCAS exams in high school. Standardized exams are a problem. A difficulty is that anything else appears to be much worse. [Update November 6th: the exams will be removed. Students in Massachusets will no more have to show their abilities in such tests. We will see how this works out. One can only assess this in a few years.] ]
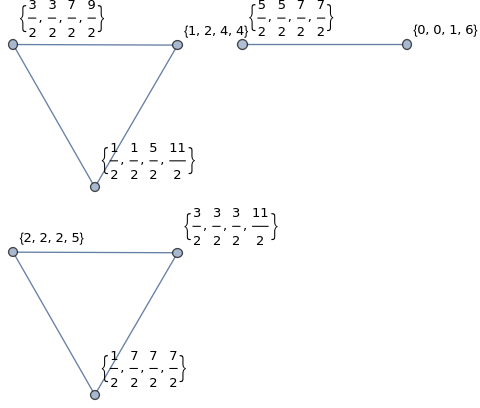
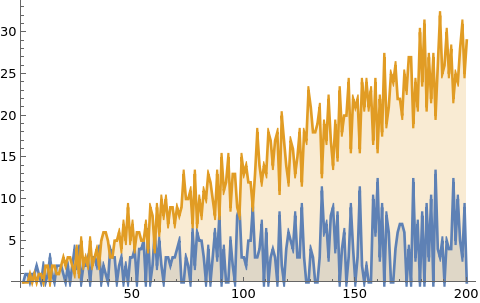
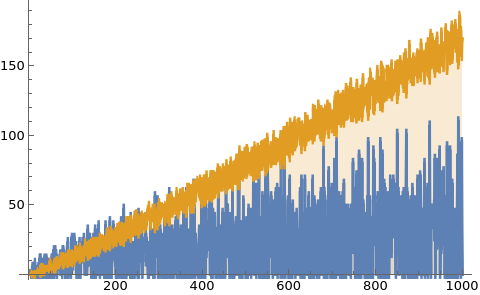
Getting back to math. When preparing for the youtube presentation I looked at my mathematica code I had written in 2016. I was able to shorten it to about a third of the length (I love short code). Part of it was to realize that Mathematica has “UnitQuaternions” already built in (I had programmed that in myself in 2016 which added already two lines) Also, some conjugations were not necessary when computing equivalence classes. Hurwitz already showed that taking left or right equivalence classes give overall the same as moving it from the right to the left induces a permutation. Here is the code producing the example from on the blackboard for p-37. 4 lines is not bad! By the way, the library call in needs to be on a separate line. There is a small bug in mathematica which would lead to complaints: loading in the library seems to take some time, and that if U is called on the same line (without a carriage return, in a notbook this is automatically changed but it is not if copy paste into the kernel), it seems not have yet have “learned” the Quaternion library. Libraries in general can be a curse in programming. But avoiding them can also be problematic. In this case, because after loading Quaternions, variables like J become known like by default imaginary unit I. You can not use I, D (derivative) or N (numerical) or E (Euler constant) as variables in Mathematica because they are known and frozen in .When loading in Quaternions, also J,K become locked as now I,J,K are the quaternion units. About the code, when using larger primes and investigating the components, one could for example type BinCounts[Map[Length, ConnectedComponents[Hadrons[1037]]]] in order to get the number of Mesons and Baryons for each prime. The number of Baryons grows about 3 times as fast. Both seem to fit roughly linearly. The fluctuations for the Mesons appear bigger.
Import["Quaternions`"];
U=UnitQuaternions; H[p_]:=PowersRepresentations[4p,4,2]/2; q[x_]:={x[[1]],x[[2]],x[[3]],x[[4]]};
abs[X_]:=Map[Abs,X]; Conjugates[X_]:=Map[q,Union[Map[Sort,Map[abs,Table[ToQuaternion[(X.{1,I,J,K})]**U[[k]],{k,24}]]]]];
Hadrons[n_]:=Module[{V=H[n],R,e,Q},e=Flatten[Table[Q=Conjugates[V[[k]]];Table[V[[k]]->Q[[l]],{l,Length[Q]}],{k,Length[V]}]];
R=Select[e,#[[1]]!=#[[2]] &]; UndirectedGraph[Graph[V,R]]]; GraphPlot[Hadrons[37], VertexLabels -> Automatic]Let’s look on how many Hadrons and Baryons there are for each prime.
F[n_]:=Module[{A=Map[Length,ConnectedComponents[Hadrons[Prime[n]]]]},Table[Length[Position[A,k]],{k,2,3}]];
ListPlot[Transpose[Table[F[n],{n,200}]],Filling -> Bottom, Joined -> True]