[Update, March 20, 2018: see the ArXiv text. See also an update blog entry with some Mathematica code. More mathematica code can be obtained from the TeX Source of the ArXiv article.].
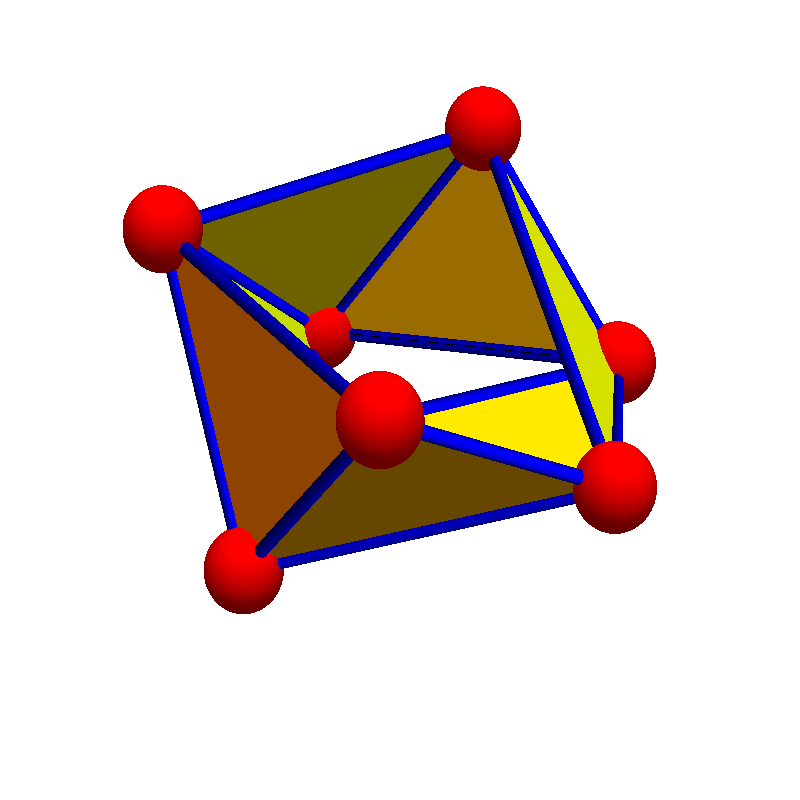
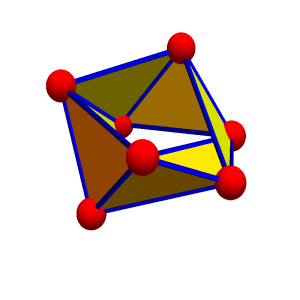
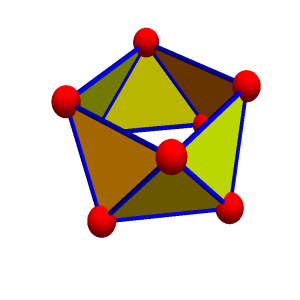
Classical calculus we teach in single and multi variable calculus courses has an elegant analogue on finite simple graphs. The discrete theory is completely analogue, Stokes theorem is almost tautological and simplicial cohomology is easy to compute just by finding the nullity of some Laplacians. Taylor expansions on graphs are just wave equation solutions on graphs. Any partial differential equation which is based on the Laplacian can be considered on an arbitrary network. While multi-variable calculus in 2 or 3 dimensions is quite old (Stokes, Ampere, Green, Gauss), the higher dimensional calculus came surprisingly late. The reason is that first, linear algebra, tensor calculus and especially multi-linear algebra had to be developed which was necessary because we are rather clumsy in accessing lower dimensional parts of space without sheaf theoretical constructs like differential forms. In higher dimensions, the frame work of differential forms in arbitrary dimensions had been formalized first by Élie Cartan around the same time than Poincaré created algebraic topology while simultaneously developing then also discrete calculus. Both in the continuum as well as in the discrete, the calculus is tied to the notion of Euler characteristic. This is visible when looking at theorems like Gauss-Bonnet-Chern (in differential geometry), Poincareé-Hopf (in differential topology), Brouwer-Lefschetz-Hopf (fixed point theorem) or Riemann-Roch (in algebraic geometry) which tap into various parts of calculus: curvature, indices of critical points, or Brouwer indices or the dimension of linear systems to divisors need calculus for their definition) Euler characteristic is the only quantity which is invariant under refinements of the geometry (Barycentric refinements) and is a linear valuation in the sense of integral geometry. But this uniqueness result (which has been proven and re-proven again and again by various mathematicians) does not exclude that nonlinear quantities exist which play the analogue role. Such quantities exist in the form of Wu characteristics. They all satisfy natural counting principles like that w(G x H) = w(G) w(H) and w(G + H) = w(G) + w(H), if x is the Graph product and + the disjoint union of graphs. Now, since Euler characteristic can be computed using calculus too. The reason is given by Euler-Poincaré relations. There is the natural question now, whether there is a calculus which belongs to Wu characteristic. Such a calculus indeed exists and so far, I don’t know whether it is related to something analogue in the continuum. What is interesting about this “interaction calculus” is that it leads to a cohomology which can “see” things which traditional cohomology (Simplicial, Cech or de Rham cohomologies) can not see. When doing computations with this cohomology it appeared that it can distinguish the cylinder and Möbius strip. Simplicial cohomology (which is by de Rham equivalent to the cohomology of traditional calculus) can not do this without taking Z2 target group (Stiefel-Whitney classes). A case study [PDF] gives a detailed computation.
 |