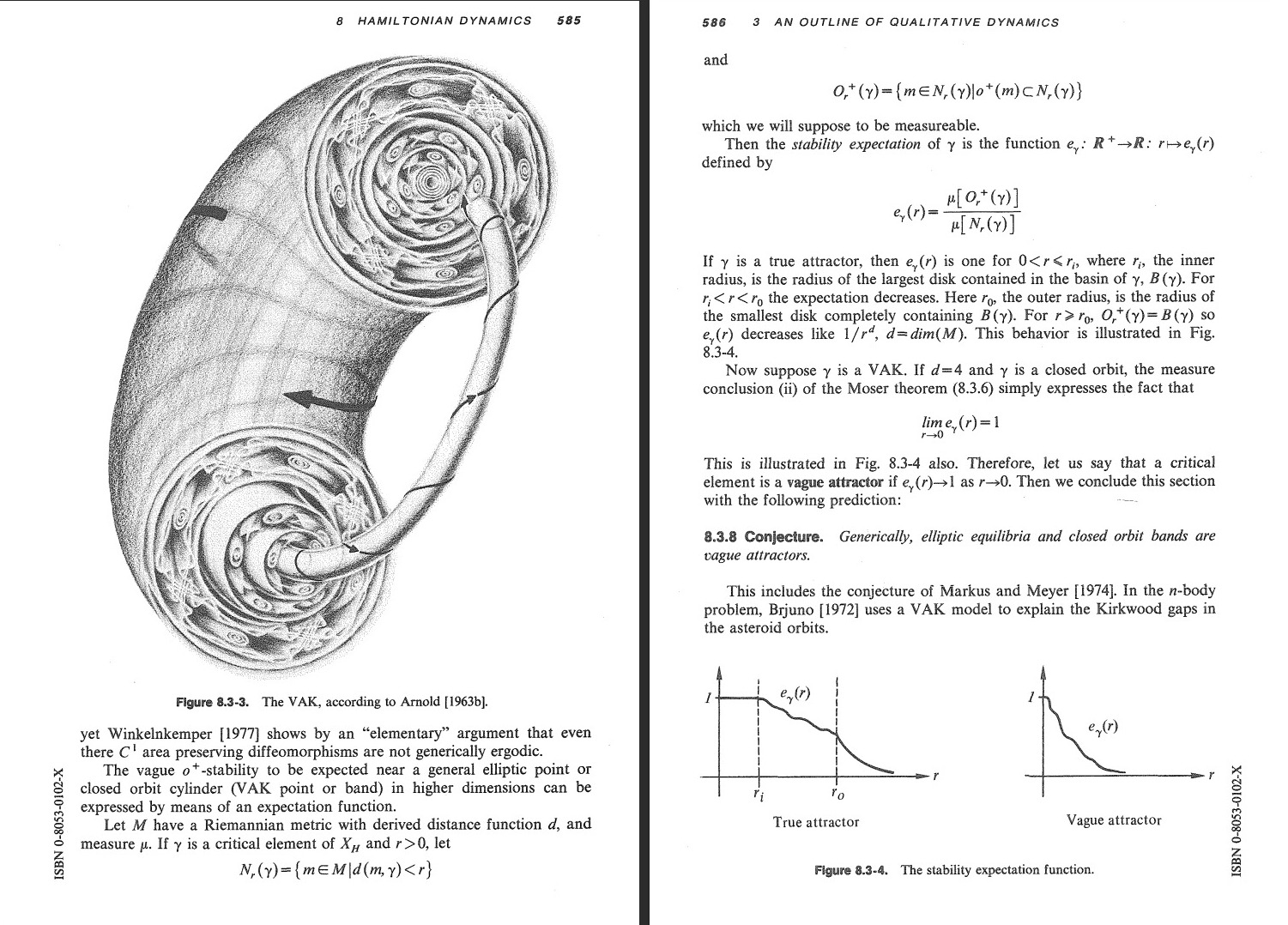
Something about the pendulum differential equation (https://arxiv.org/abs/2306.10653). Analyticity could be helpful in ergodic theory because if Lyapunov exponents are parametrized by analytic functions, they are subharmonic. I had used subharmonic techniques of Herman already in my thesis. The idea was summarized in here in a Harvard math table talk of 2004 [PDF]. A major open problem in Hamiltonian dynamics is to confirm the VAK picture of Kolmogorov. The following picture appears in the textbook of Abraham and Marsden and is due to Arnold. The picture (called Coexistence problem by Strelcyin) is to show that there are two dense sets A,B, where on A the dynamics is integrable and where on B the dynamics has positive entropy. Integrability can be defined in a spectral way (See this talk [PDF] from 2002): a system is integrable on a subset A if every invariant measure on A defines a dynamical system with pure point spectrum. Also mentioned in the talk was that Ahlfors used to be in the Harvard office 434 which made room to the common room in 2011. (See this page). Lars Ahlfors was since 1946 professor at Harvard and lived in Winchester (Source: Crimson).
What does this has to do with quantum calculus? One obvious relation is that once we see the pendulum differential equation as a translation on an elliptic curve, we can obviously just see the translation on any elliptic curve as a “pendulum”. This can also be a finite elliptic curve! The upshot is that the pendulum dynamics is given by a family of elliptic curves. Every initial position and velocity defines an elliptic curve. In very special situations, this curve is singular. This happens in the dynamics if the pendulum has just enough energy to get to the top. In that case the Weierstrass function value will go to infinity and the argument converges.