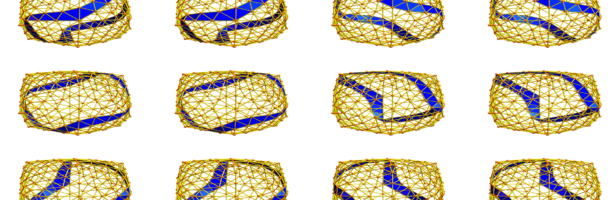
Given a q-manifold, we have a geodesic dynamics T:P -> P, where P is the oriented frame bundle. Most geodesics are not simple but we can look for the number of simple closed geodesics and so investigate questions close to the Ljusternik-Schnirelmann theme in the classical setup. For any 2 manifold there always at least 3 different simple closed geodesics. In the discrete there are examples with none but that might actually just happen only for small manifolds. We still need to investigate this question “How many simple closed geodesics are there in a given finite q-manifold?” Here are all 12 simple closed geodesics in a small sphere. The video this week had the title “solid Klein bottles” because in 3-manifolds it is possible that geodesics are solid Klein bottles. In three dimensions, the classification of simple closed geodesic paths is clear because the boundary of the geodesic tube is a flat 2-manifold and in two dimensions, the flat 2-manifolds are classified. The solid Klein bottle can be obtained by taking the topological product of the Klein bottle with an interval and identifying the two Klein bottle boundaries to have one boundary surface.
[One of the issues which could lead to cases with less than 3 in the discrete is that the geodesic returns back to itself after some rotation. I for now have rejected those and only looked at cases where the simpices along a closed geodesic in the frame bundle are not a cover of the actual geodesics. What would be totally cool of course is if we could prove there exists one closed geodesic for every rotation possible as it would give for a 2-sphere at least one simple geodesics. On a q-sphere we would have q!/2 different geodesics in case there would be simple mechanism assuring that there is always a solution for any rotation type. But that can not work as we see for the smallest 3 sphere (16 cell) that there are are 48 simple closed geodesics or length 8. And for the 4-sphere (32 chamber) that there are 384 closed geodesics of length 10 (there are 32*120 = 32*5! = 3840 elements in the frame bundle. We have also seen discrete 2-spheres with ergodic geodesic flow meaning that we have no simple closed geodesics.]
Yesterday, I talked about the topology of simple closed geodesics. This can already be interesting as in q-dimension, geodesics are a tube with boundary and we can look at the topology of the tube or boundary. I decided to look at that using quadratic cohomology as this produces topological invariants. In two dimensions, the geodesics can be either cylinders or Moebius strips. In an orientable manifold, they are always cylinders. We see a small 2-sphere above and all 12 simple closed geodesics, they are all cylinders, 2-manifolds with two circular boundaries. On a Klein bottle, we can have cases where the boundary of the geodesic is a single closed curve. That happens if the goedesic is a Moebius strip.
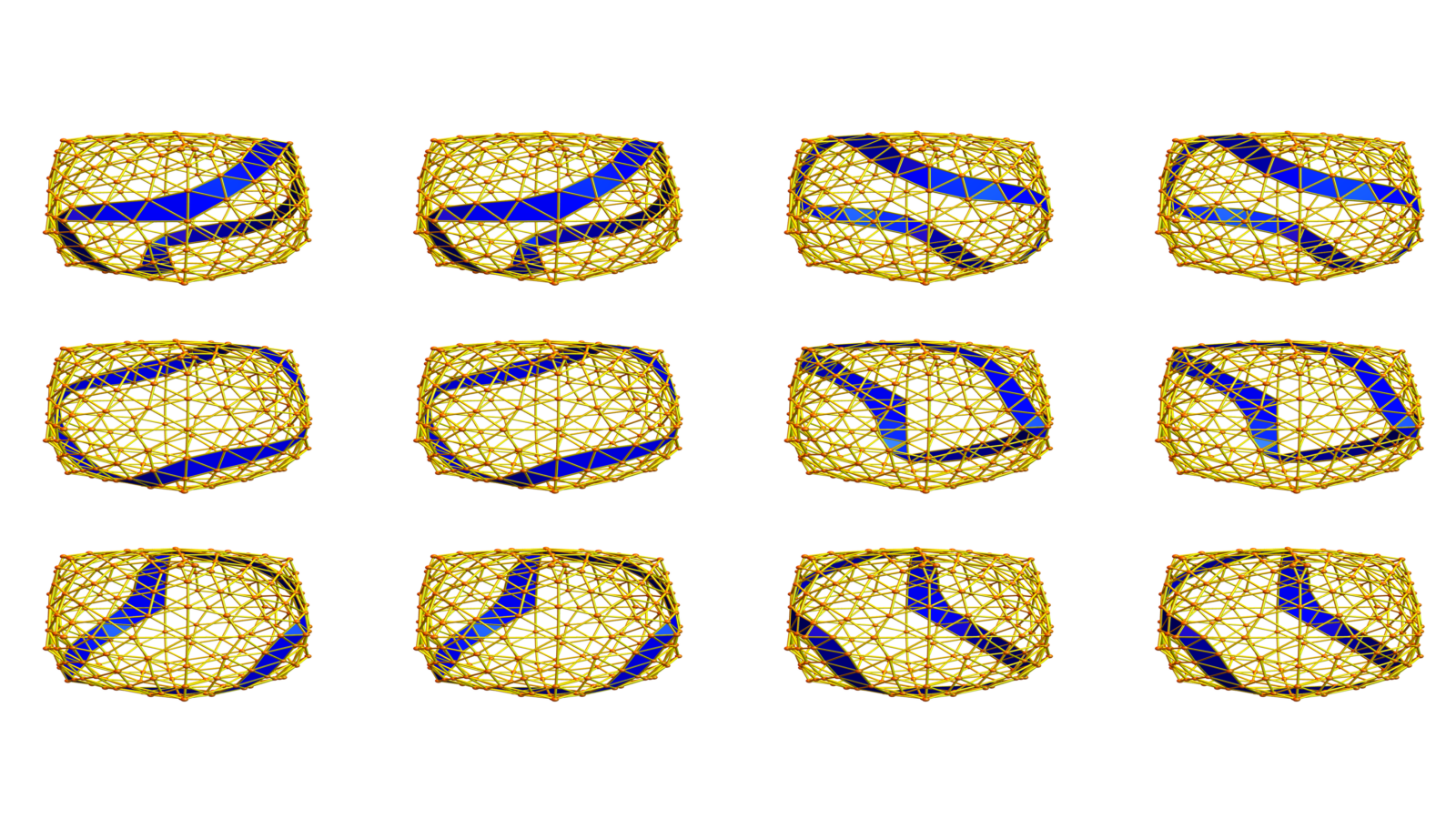
In 3 dimensions, the boundary of a geodesic is always a flat 2-manifold. Being geodesic implies that the boundary surface is flat everywhere. The Euler characteristic especially is zero and there are only two 2-manifolds with Euler characteristic 0: the Klein bottle or the 2-torus (a cover of the Kleinbottle) . Also here, we can using quadratic cohomology distinguish the geodesics themselves, without looking at the boundary. We can already in the case of the Moebius strip and the cylinder distinguish the two topological spaces by looking at the boundary. What is interesting is that we can distinguish the solid torus and the solid Klein bottle cohomologically using quadratic cohomology. Simplicial cohomology of course can not distinguish the solid torus and the solid Klein bottle because both are homotopic to a circle. Simplicial cohomology is quite “stupid” especially here when looking at simple closed geodesics.
Quadratic cohomology can distinguish the solid torus and the solid Klein bottle.
The proof is just a computation. We see in the Solid Klein bottle case the Betti vector (0,0,0,1,1,0,0) while the solid torus has (0,0,0,0,0,0,0). This is analog to the case in dimensions 2, where the cylinder has quadratic cohomology (0,0,1,1,0) and the moebius strip has quadratic cohomology (0,0,0,0,0),