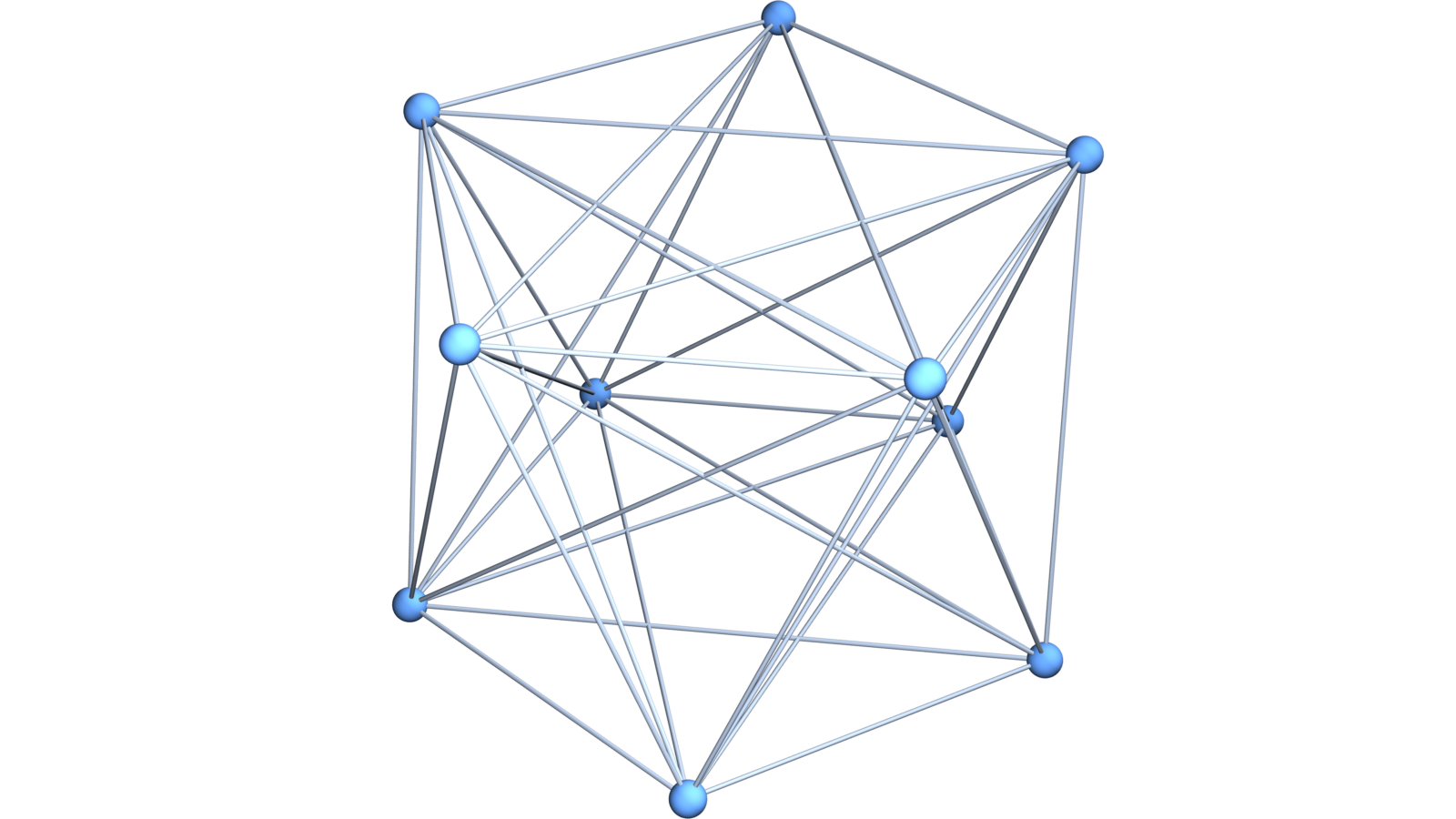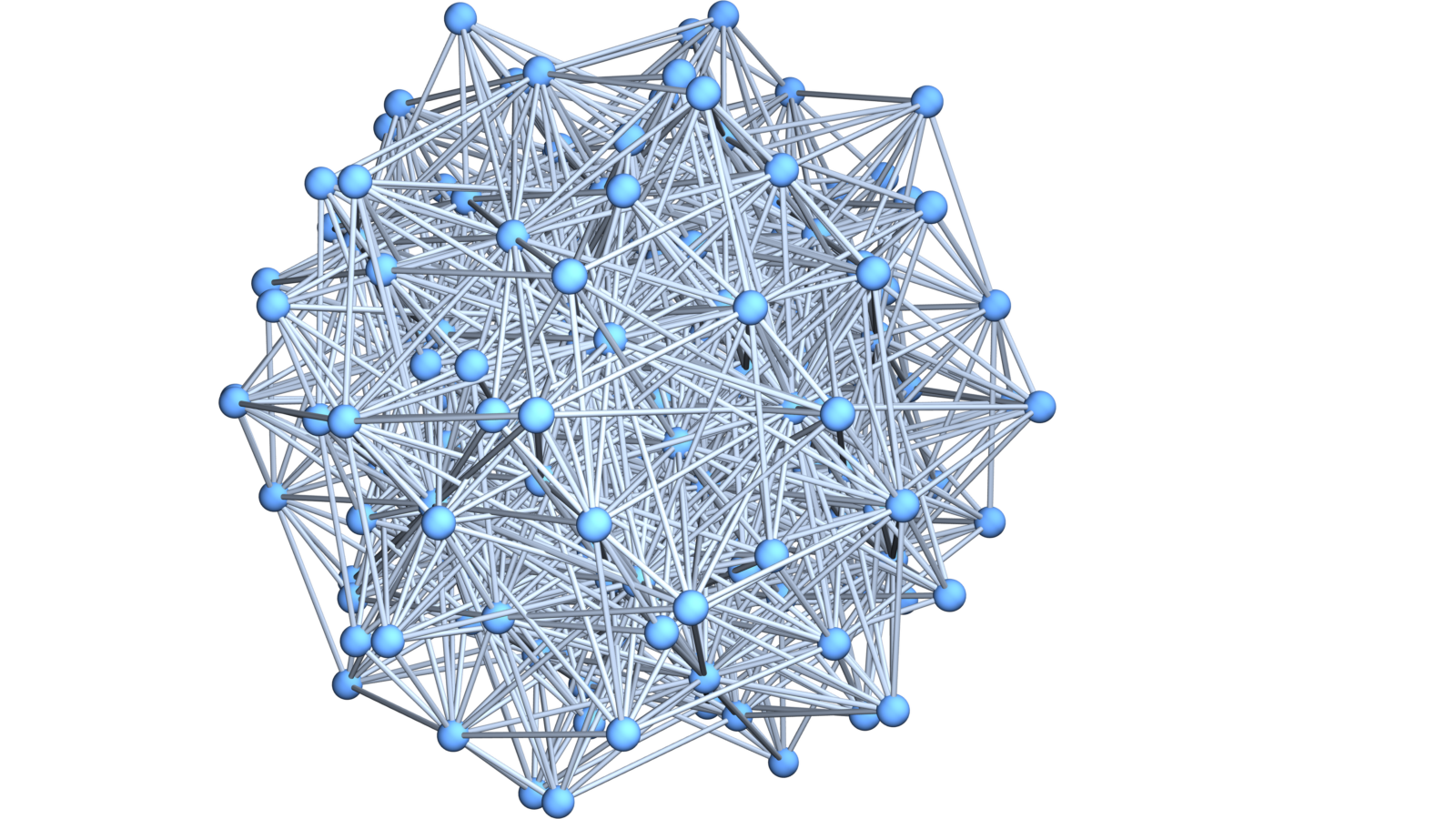
More on Soft Barycentric Refinement

The definition of soft Barycentric refinement needed adaptation so that it preserves manifolds with boundary. If G is a finite abstract simplicial complex. The Barycentric refinement is the Whitney complex of the graph in which G are the vertices and where two points are connected, if one is contained in the other. The soft Barycentric refinement is obtained from the Barycentric refinement by collapsing at interior facets of codimension 1. To the right, we see the first 2 soft Barycentric refinements of $K_4$ . They are 3-balls. The left one has the f-vector (15, 50, 60, 24) the right one (113,544,792,360). The next refinement would have f-vector (1161, 6344, 9936, 4752). Note that the left is identical to the Barycentric refinement of $K_4$ . But its Barycentric refinement would be larger and have f-vector (149, 796, 1224, 576). But it has the same boundary. The density of states of the soft Barycentric refinements in dimension d looks close to the density of the states of the Barycentric refinements in dimension d-1. Below we see some soft Barycentric refinements of a prism $C_{10} \oplus S^0$ .

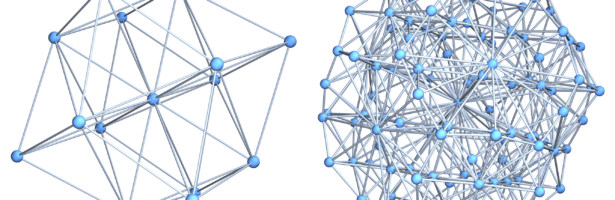
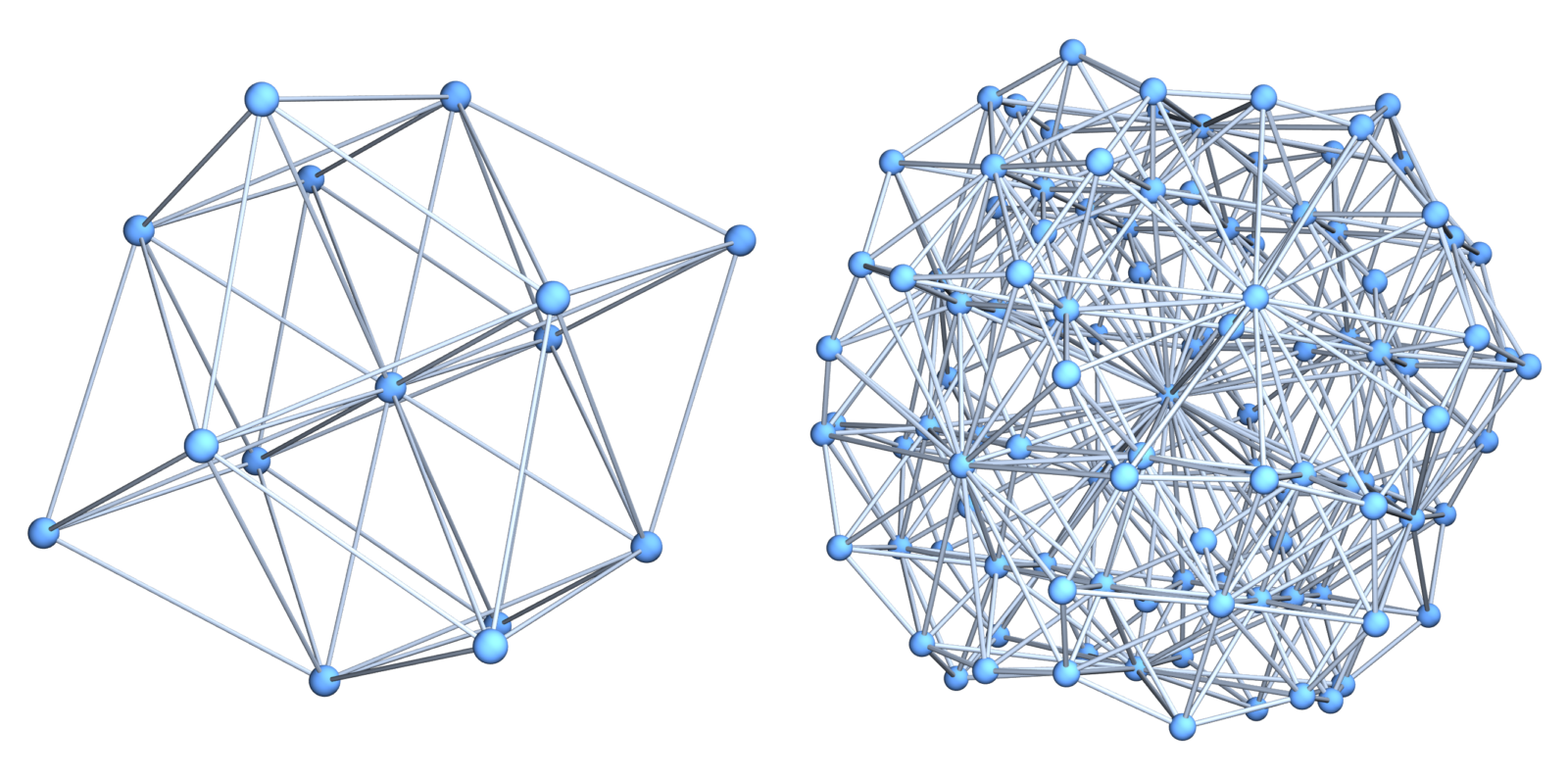
Here we see some soft Barycentric refinements of a prism graph. What is nice about soft Barycentric refinement is that it preserves vertex degrees and only adds vertices which have zero curvature. The curvature spectrum of Soft Barycentric refinements in dimension 2 stays the same.

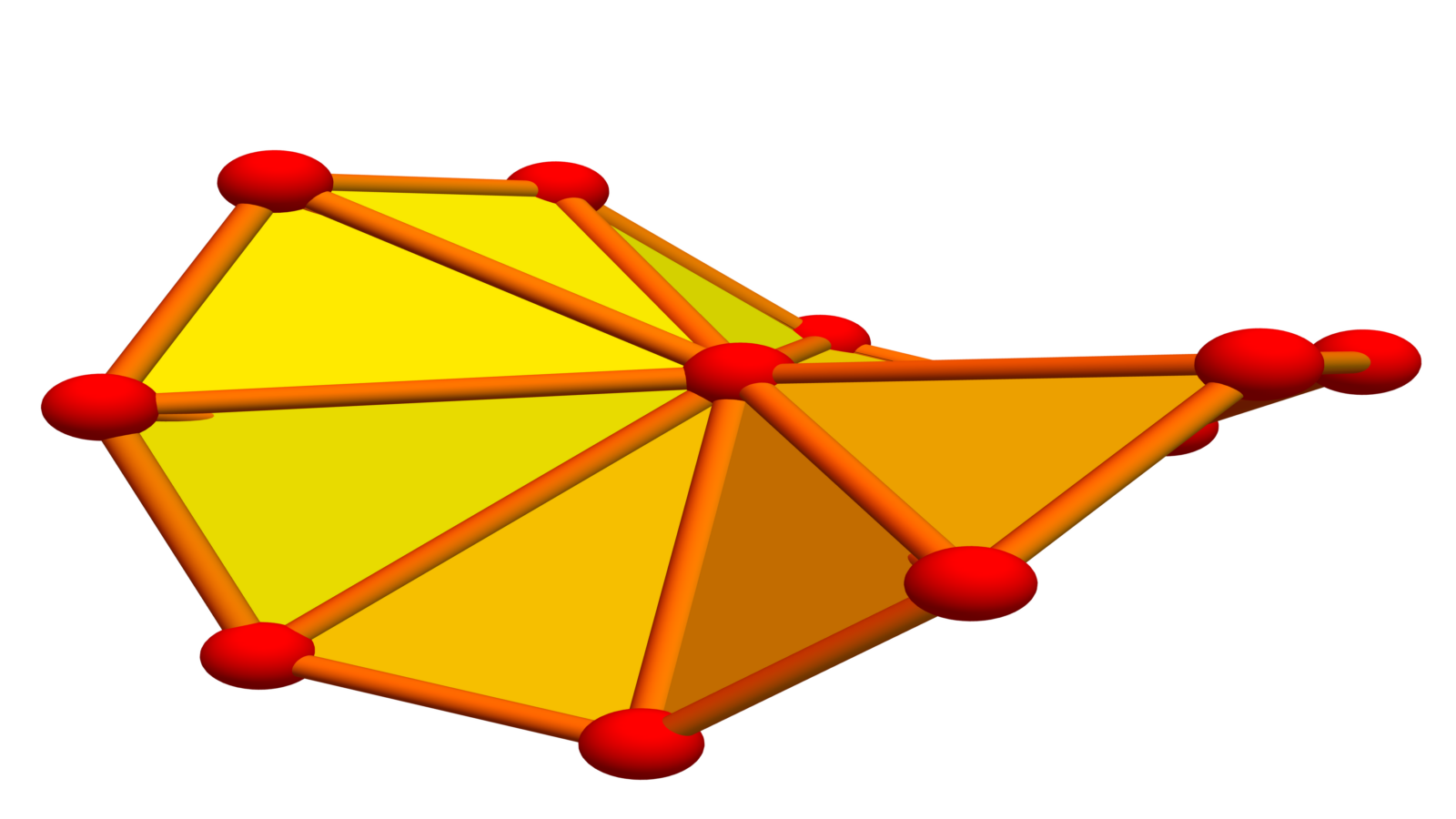
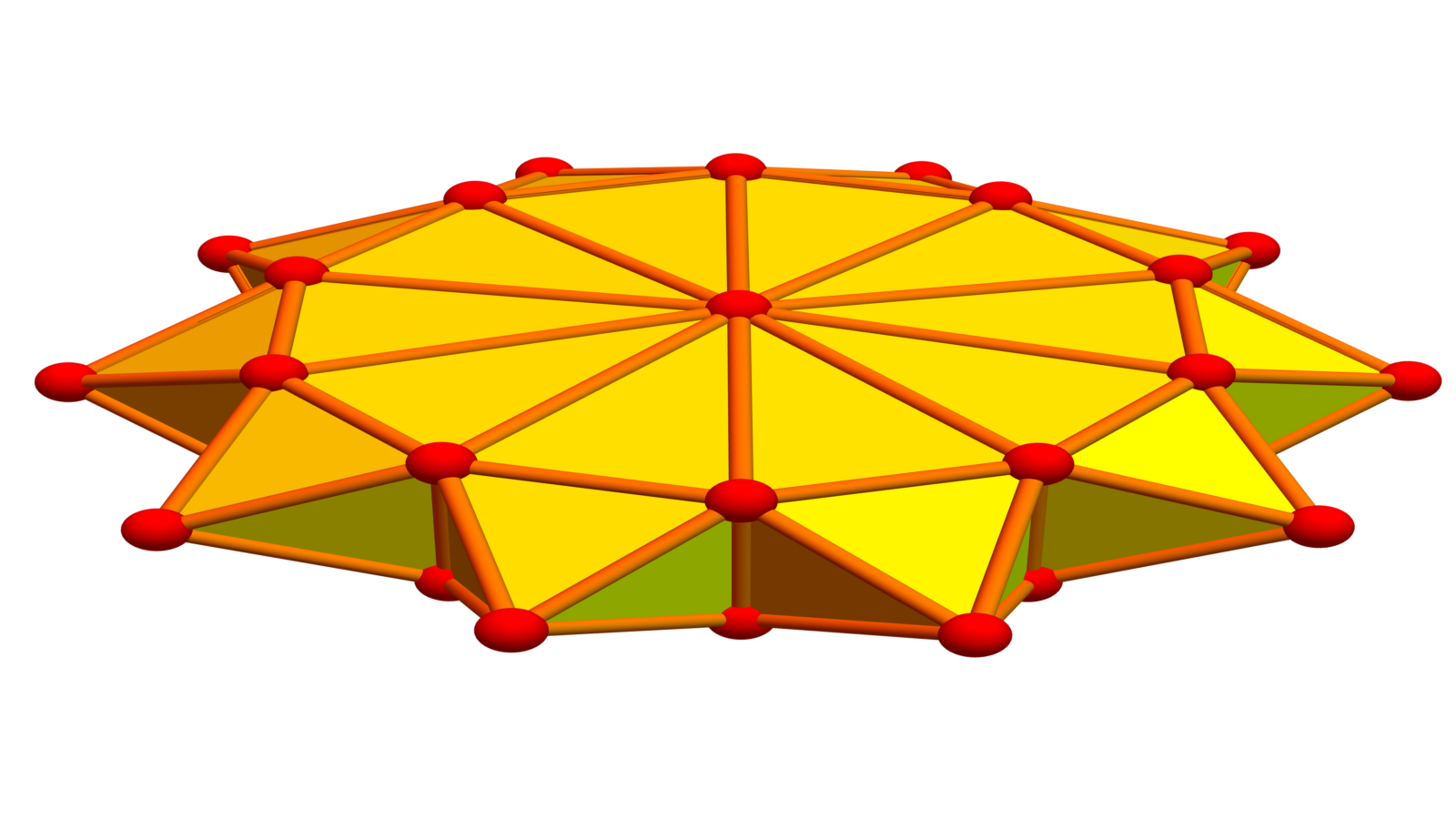
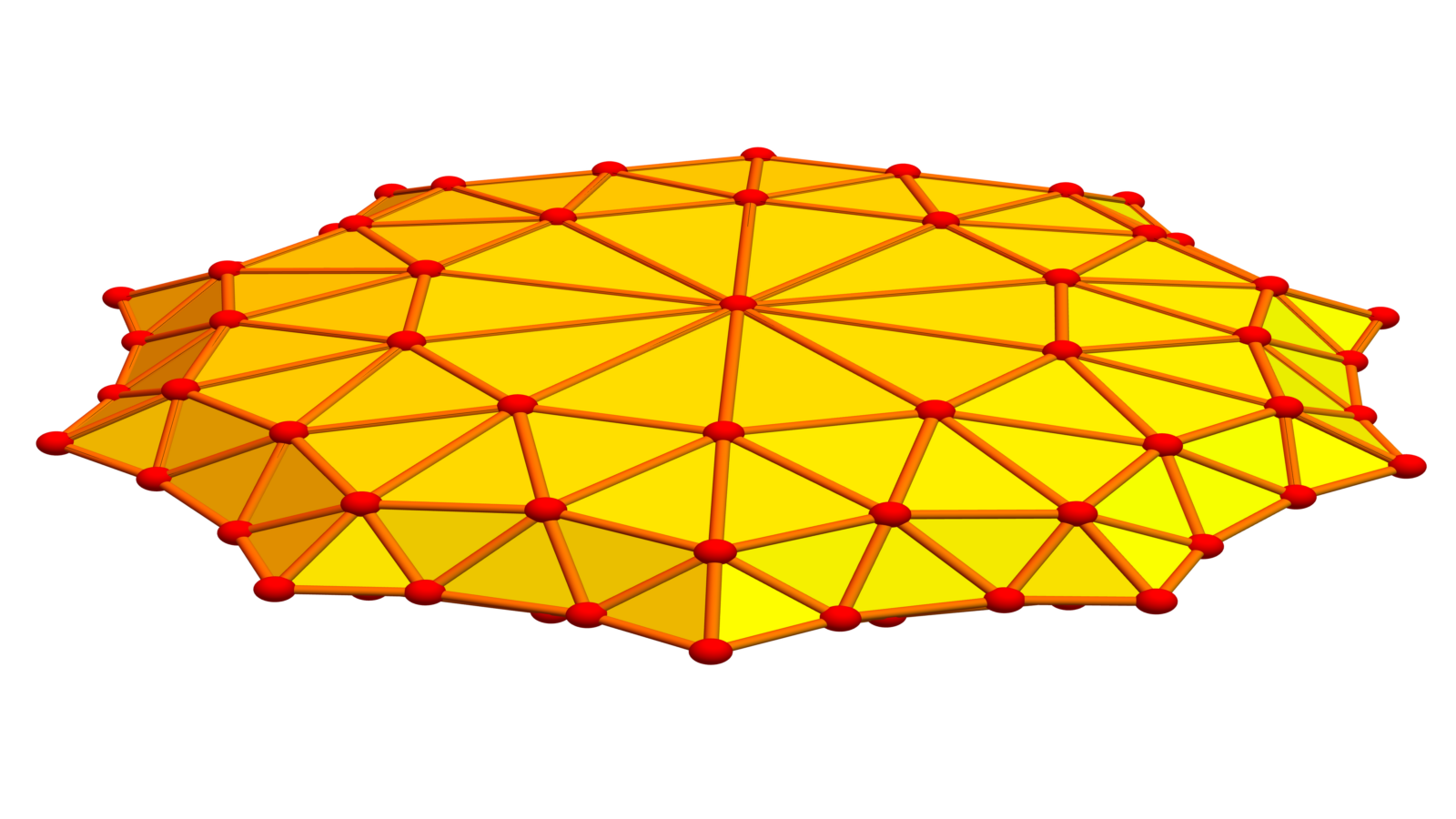
We mention the result $\delta \phi(G) = \psi \delta G$ , if $\psi$ is the Barycentric refinement and $\phi$ the soft Barycentric refinement. I had been more concerned with the Barycentric limit but here is an other interesting fact:

Similarly as soft Barycentric refinement keeps curvature bounded for 2-dimensional complexes, the soft Barycentric refinement keeps Ricci curvature bounded for 3 dimensional complexes! We mean with Ricci curvature curvatures of the unit spheres. While the unit spheres grow, the maximal curvatures of these spheres does not. Here is the 3-sphere $K_{2,2,2}$ and its 2 soft Barycentric refinements:

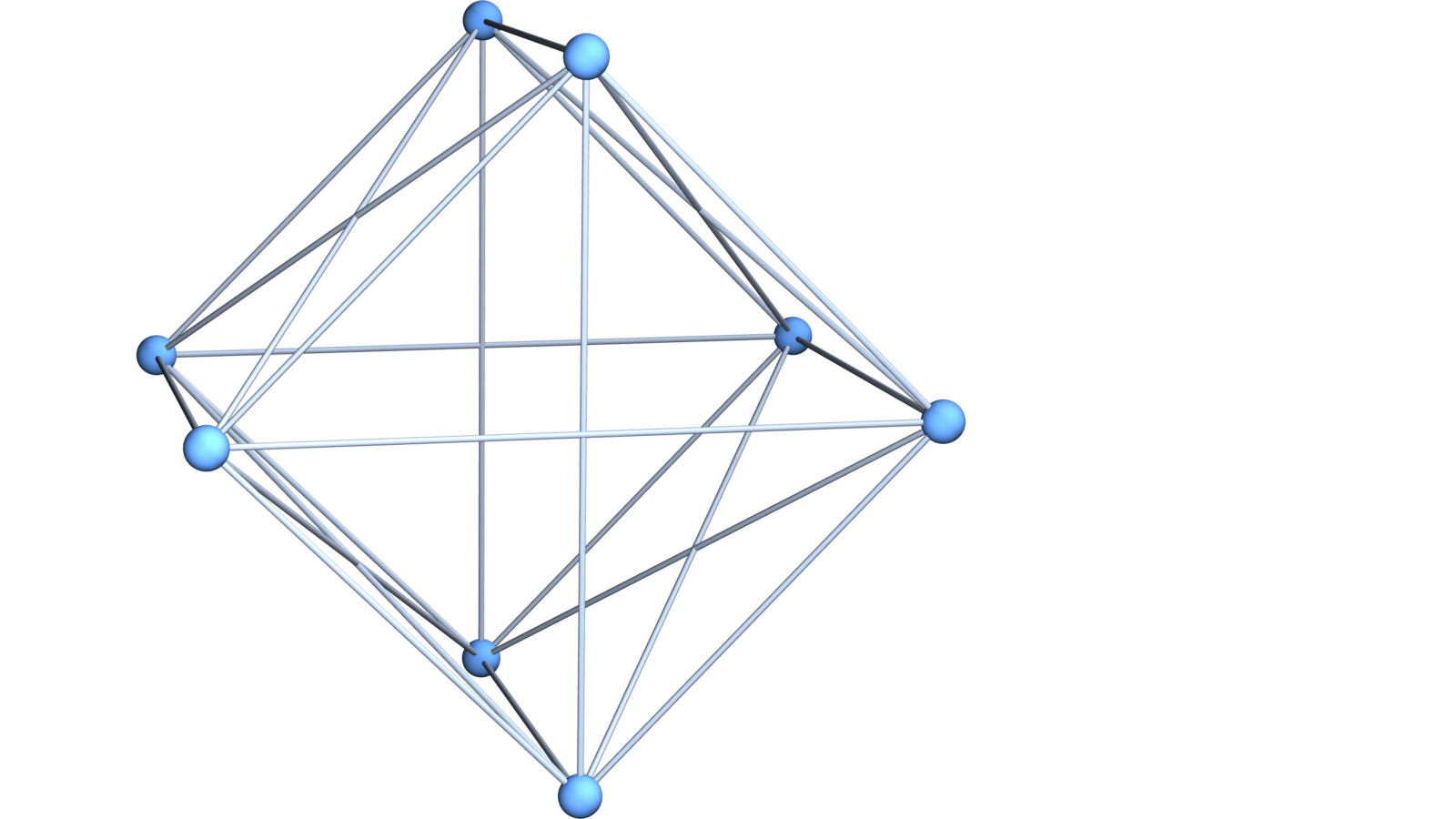
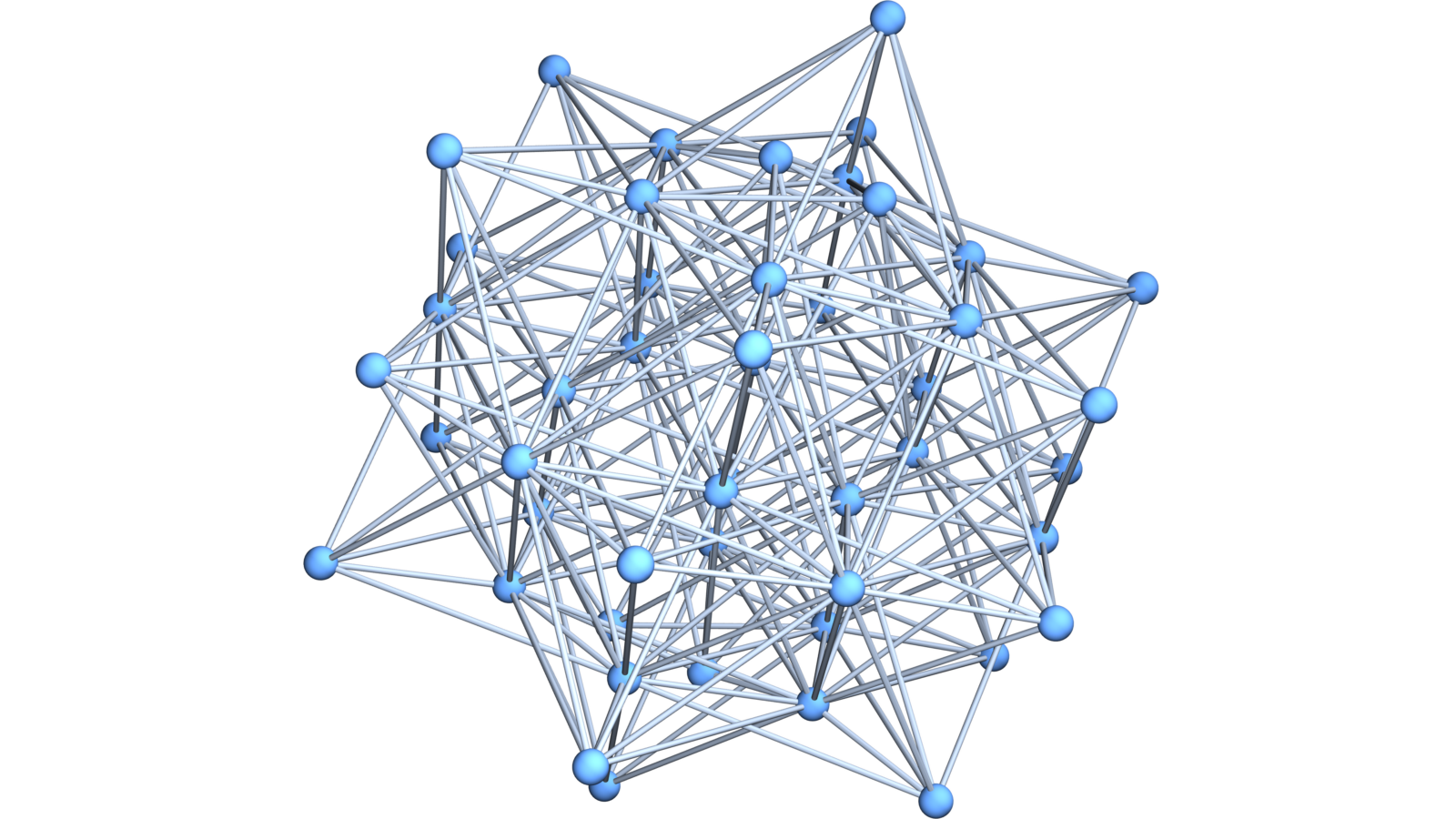
Similarly the Ricci curvature of a 4 dimensional complex stays bounded. Here we see the 4-sphere $K_{2,2,2,2}$ and a soft Barycentric refinement. The Ricci length of the intersection of 3 adjacent unit spheres is mostly 6 meaning that the sphere is mostly Ricci flat. Even more exciting is probably that the Ricci curvature for 4 manifolds stays bounded when doing soft Barycentric refinement! By the way, the display hanging in the video from the board is a pretty cool gadget shows the two major equations from general relativity. One can write on it with markers and it glows. Would be nice to have a large board like that.

Author: oliverknill