The sphere spectrum paper is submitted to the ArXiv. A local copy. It is an addition to the unimodularity theorem and solves part of the riddle about the Green function values, the diagonal elements of the inverse of the matrix 1+A’ where A’ is the adjacency matrix of the connection graph of the simplicial complex. The paper contains two main results. They are both completely finite and combinatorial. No continuum is involved at any moment. So, it fits well into the concept of quantum calculus, especially because connection graphs are an integral part of any discrete connection calculus:
|
Theorem 1 (Green function formula) The integer |
Proof: we prove a new proposition telling what happens when a cell is removed. The Cramer formula for the inverse of a matrix then directly shows the formula.
This is pretty cool. The Poincaré-Hopf indices are important in many places like Riemann-Roch for graphs, or Poincaré-Hopf for graphs. They are natural functionals because for spheres G, the value of i(G) is in {-1,1}. It turns out to be a character in the sphere group defined by the join operation. Note that the theorem relates two graphs, the Barycentric refinement G1 as well as the larger connection graph G’ which contains G1 as a subgraph.
The second result is also quite general. It tells that for any finite abstract simplicial complex G, the unit sphere topologies of the Barycentric refinement G1 agree with the sphere topologies of the second Barycentric refinement G2 (and so of all other Barycentric refinements). In order not to have to be bugged down what it means to be a “sphere topology” we just look at the Euler characteristic of the unit spheres:
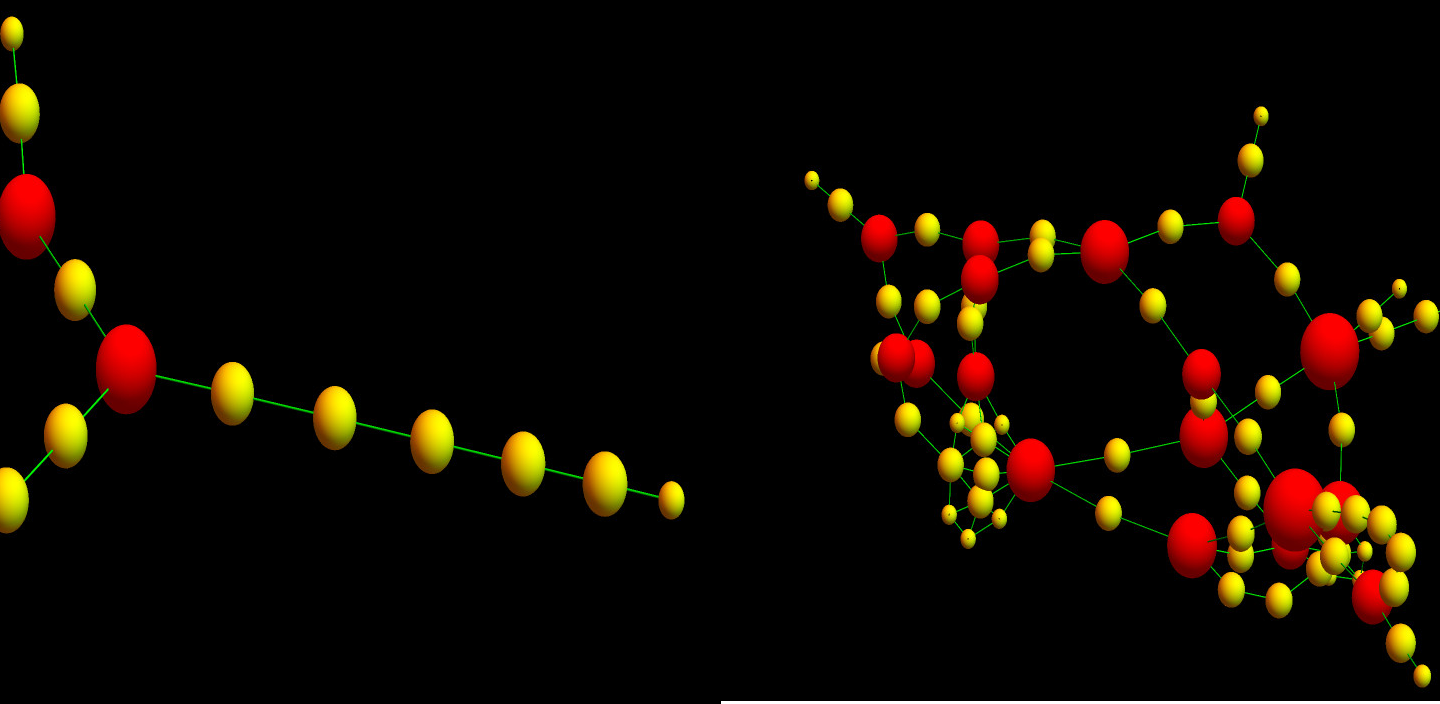
Define the sphere spectrum of a simplicial complex as the set of possible values i(S(x)), where x runs over all points in the Barycentric refinement (meaning over all faces of the complex). A combinatorial invariant in the sense of Bott is a functional on simplicial complexes which has the property that it is invariant under Barycentric refinements.
The genius part of Bott’s definition is that it completely avoids the difficulty to define topological invariant for which there are myriads of different ways and notions and also which usually involves the continuum (like for example Euclidean space). For a mathematician wanting to honor quantum calculus and therefore wants to avoid any continuum notions, this notion of combinatorial invariant is perfect. It is purely combinatorial and discrete (quantized).
| Theorem 2 (Unit sphere spectrum) The unit sphere spectrum of a simplicial complex is a combinatorial invariant. It does not change under Barycentric refinement. |
Proof. One direction is easy. Every unit sphere in G1 can directly be paired with a unit sphere in G2. More work is required for the reverse. We have to show that every unit sphere in G2 has a topologically equivalent unit sphere in G1. In order to do that we analyze unit spheres more carefully. We can decompose it into a stable and unstable part (this is analoguous to hyperbolic dynamics or Morse theory, and it was also here that a dynamics background was helpful for me, especially the lectures of Oscar Lanford). Now the stable part can be analyzed pretty well. It is always a sphere and it is here that the arithmetic of networks is helpful. The unstable part can also be matched, if we chose the right vertex in G1. This was a bit of a riddle. Since every vertex in G2 corresponds to a simplex in G1 which consists of simplices for which every vertex again is a simplex in G, we have a nice structure. The stable part can either be described as an intersection of spheres or then as the join or some spheres.
The just sketched proof gives a reason why we got so interested in the Zykov addition in graph theory. Also mentioned in the paper is the sphere arithmetic given by the join and multiplication already mentioned. Also the spectral part has been merged in. There are so many nice things about the Zykov addition: one can explicitly give the f-vector of the sum, one can explicitly give the Euler characteristic of the sum, the sum preserves spheres, there is an inequality for inductive dimension similarly as for the Cartesian product, there is a Kunneth formula for cohomology and there are results about the spectrum. At the very end, we added a remark about the spectrum of the highest form Laplacian of the sum of two graphs. It is pretty cool that the spectral values add there.
It should be added that the results are not stated in maximal generality. One could formulate it in the concept of more general CW complexes (simplicial complexes are a special case). But the setup also shows how one can avoid pretty well the language of simplicial complexes and instead deal with graphs like the Barycentric refinement or the connection graph. This is not new and there are other ways to visualize simplicial complexes, one being the Hasse diagram. But when comparing the intuitive simplicity of graphs, Hasse diagrams are forbidding.
Anyway, this work has actually given me a bit of more appreciation about simplicial complexes (even so also in future, I will think still in terms of graph theory as graphs are much, much more intuitive). But the structure of a simplicial complex can not be beaten in simplicity. I’m not aware of a simpler structure (except the category of sets). There is only one axiom for the set of subsets: it has to be closed under taking subsets. If one compares with algebraic notions like groups or rings or measure theoretical notions like sigma algebras or order structures or topologies, this is much simpler. Its just amazing how much structure there is in such a simple setup.
Here is a picture illustrating the sphere spectrum, the values of i(x) are encoded in the size of the node: