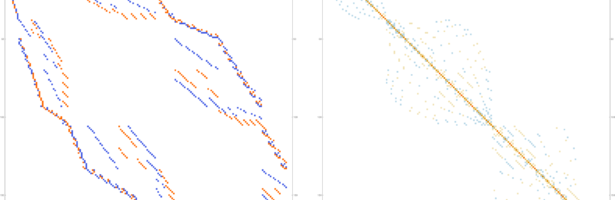
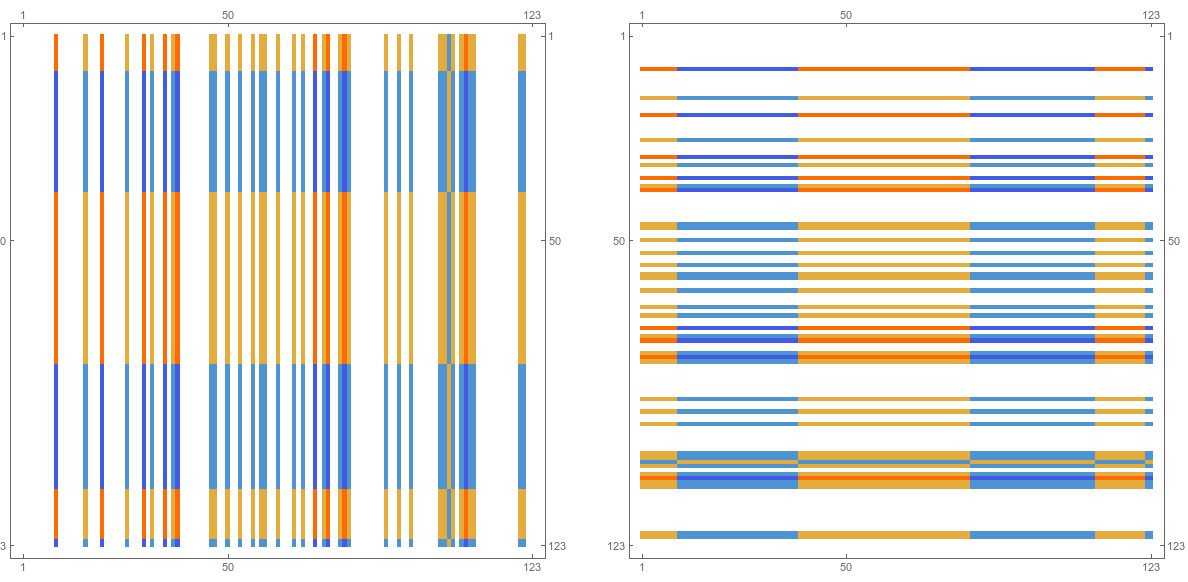
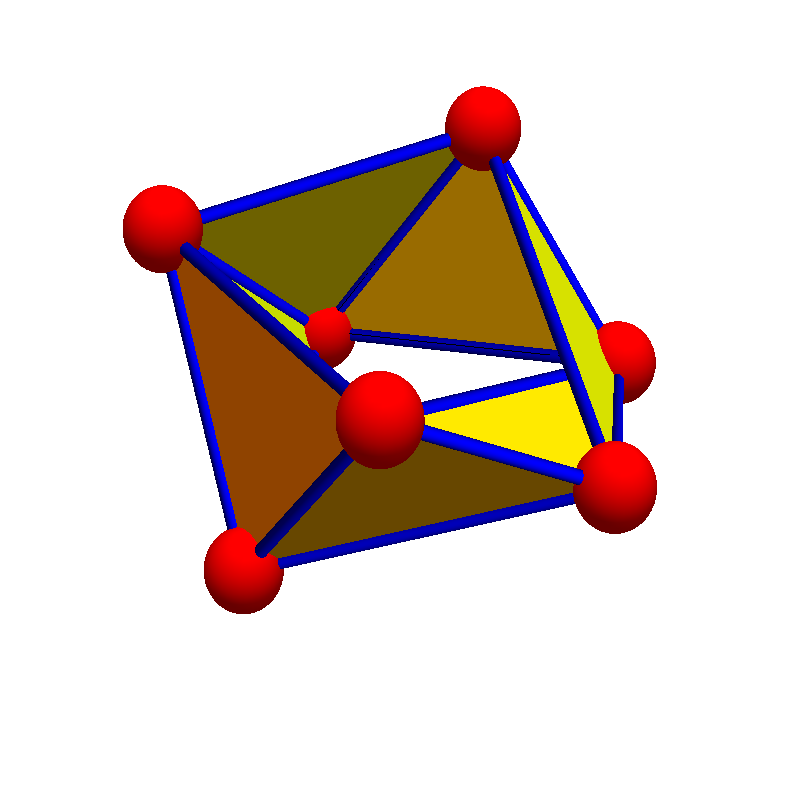
Quadratic Cohomology
I looked at a quadratic cohomology example. For theoretical backgroun, see the ArXiv paper “Fusion inequality for quadratic cohomology”. It is the case when U is a union of two disjoint smallest open sets in a 2-sphere for which I take the Icosahedron, one of the Platonic solids and a …