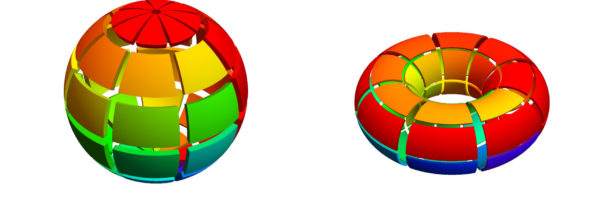
Curvature is a local notion in a finite geometry that adds up to a topological invariant. This is Gauss-Bonnet. I’m only really interested in curvatures that satisfy this exactly. This does not exclude sectional curvature, the latest venture because sectional curvature integrated over a geodesic sheet is the Euler characteristic …
A 2-manifold with boundary is a finite simple graph for which every unit sphere is a circular graph with 4 or more nodes or a path graph with 3 more nodes. The boundary is the set of vertices for which the unit sphere is a path graph, the interior is …
The definition of soft manifoldss now fixed. It is only fitting to call the old discrete manifolds hard manifolds. Unlike the later, soft manifolds can be multipied. They define a subring of the Shannon ring.
We report on some progress on analytic torsion A(G) for graphs. A(G) is a positive rational number attached to a network. We can compute it for contractible graphs or spheres.
A major open problem in Riemannian geometry is the classification of even dimensional positive curvature manifolds with symmetry. There is a reduction theory which produces a periodic system of elements. This picture has affinity with gauge bosons in physics.
The Hopf conjectures were first formulated by Hopf in print in 1931. The sign conjecture claims that positive curvature compact Riemannian 2d-manifolds have positive Euler characteristic and that negative curvature compact Riemannian 2d-manifolds have Euler characteristic with sign (-1)d . The product conjecture claims there is no positive curvature metric …
